доведіть шо при будь якому значенні зміної x вираз x²+8x+17 набуває лише додатніх значень. якого найменьшого значения набуває цей вираз і при якому значенні x
Ответы
Відповідь:
Покрокове пояснення:
= 0 ==> D =
= 64 - 68 = -4
Якщо дискримінант від'ємний то квадратний тричлен графіком якого є парабола буде мати або тільки додатні числа, або тільки від'ємні. Хочу ще додати, що в нас a > 0, тому парабола дивиться вітками вгору, отже найнижча точка це вершина параболи,
Формула для знаходження x вершини параболи: , а y параболи знаходиться підставляючи x в функцію:
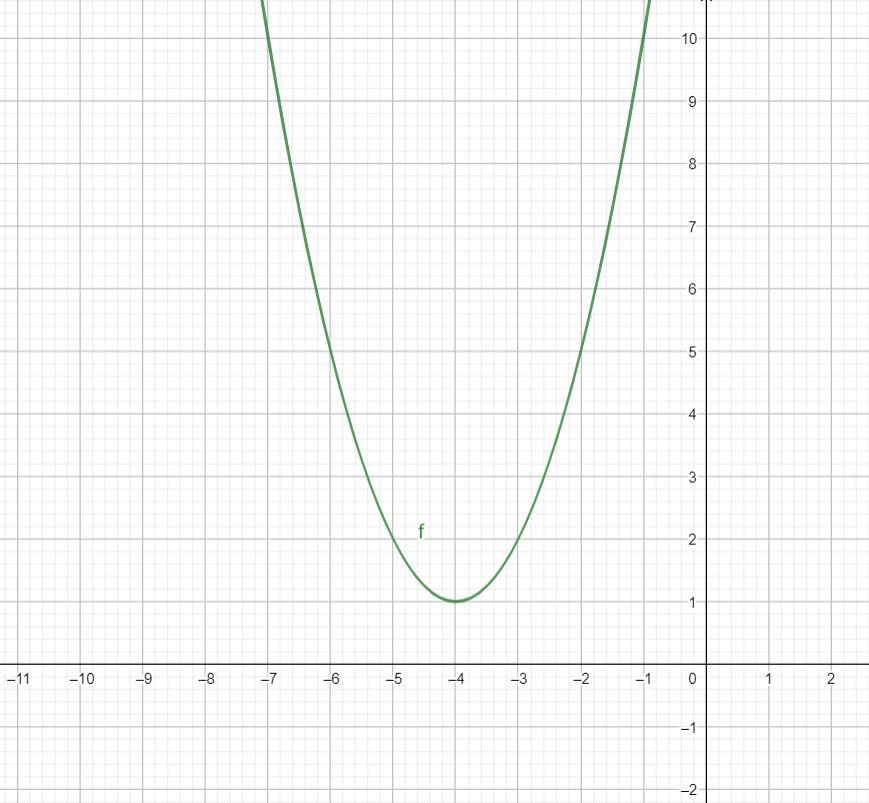
Так як дискримінант вийшов від'ємним, тобто графік параболи не перетинає вісь x, а вершина параболи має такі кординати: (-4;1) і парабола "дивиться" вгору, тому вираз може набувати тільки додатніх значень і в цьому випадку найменше значення функції, тобто найменший y це буде y вершини параболи
Можна це перевірити підставляючи в функцію різні x
x = 0, тоді = 0 + 0 + 17 = 17
x = -1, тоді = 1 - 8 + 17 = 10
x = -2, тоді = 4 - 16 + 17 = 5
x = -3, тоді = 9 - 24 + 17 = 2
x = -4, тоді = 16 - 32 + 17 = 1
x = -5, тоді = 25 - 40 + 17 = 2
Малюнок: