Предмет: Алгебра,
автор: kbohonova
мне нужно решение уравнения через дискриминант с подробным решением и объяснением.
Приложения:
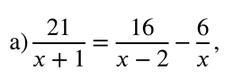
Ответы
Автор ответа:
2
Ответ:
Корни уравнения:
Объяснение:
Требуется решить уравнение:
Так как переменная в знаменателе, необходимо определить ОДЗ:
х + 1 ≠ 0 ⇒ х ≠ -1
х - 2 ≠ 0 ⇒ х ≠ 2
х ≠ 0.
Перенесем слагаемые из правой части в левую часть, поменяв знаки на противоположные:
Приведем к общему знаменателю и раскроем скобки в числителе:
- Дробь равна нулю, если числитель равен нулю.
Приведем в числителе подобные члены и приравняем к нулю.
Найдем дискриминант:
√D = √4624 = 68
Теперь найдем корни:
Корни уравнения:
kbohonova:
большое спасибо :)
Похожие вопросы
Предмет: Русский язык,
автор: 1960WALEN1960
Предмет: Английский язык,
автор: angliskii1
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: lor357
Предмет: Английский язык,
автор: sadnesskills