Предмет: Геометрия,
автор: 375295483121katya
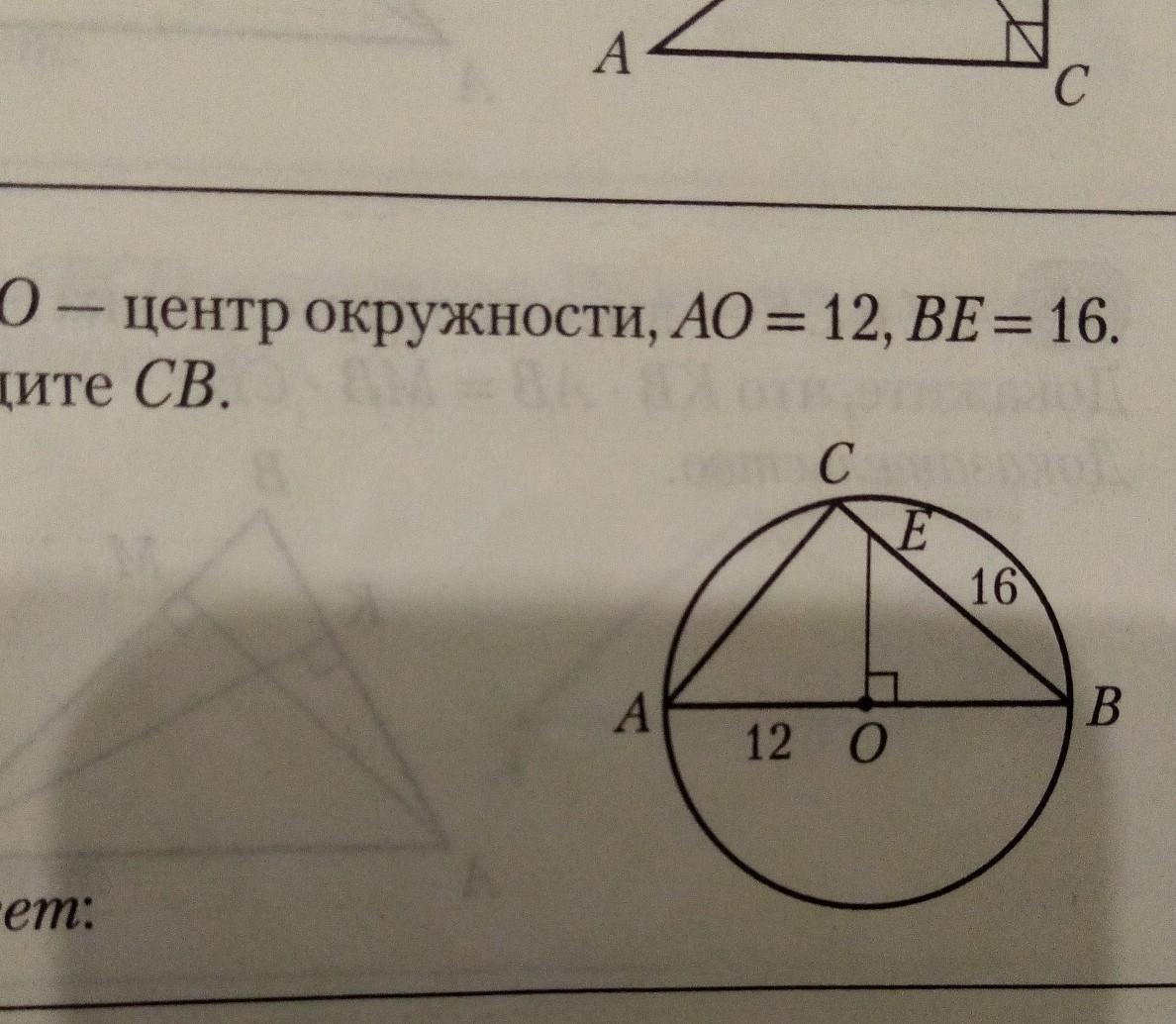
о центр окружности АО равно 12 Б равно 16 найти CB
Приложения:
Ответы
Автор ответа:
1
Центр окружности, описанной около ∆ АВС, лежит на основании АВ. Из О возведен перпендикуляр до пересечения с ВС в т.Е. ВЕ=16, АО=12. Найти ВС.
Ответ: 18 ед. длины
Объяснение:
Рассмотрим ∆ АСВ и ∆ ЕОВ. Они прямоугольные ( угол ЕОВ=90° - дано, угол АСВ=90° – вписанный, опирается на диаметр АВ), с общим острым углом АВС. Прямоугольные треугольники с равным острым углом подобны.
Из подобия треугольников следует отношение:
АВ:ВЕ=ВС:ВО, =>
2•12:16=ВС:12, откуда ВС=18 (ед. длины)
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: hasanka54
Предмет: Русский язык,
автор: анна1349
Предмет: Английский язык,
автор: мария1429
Предмет: Математика,
автор: 1415886k
Предмет: Математика,
автор: katrin5092