Предмет: Геометрия,
автор: moshonkamonka
Упражнение 13 из 20
Реши задачу.
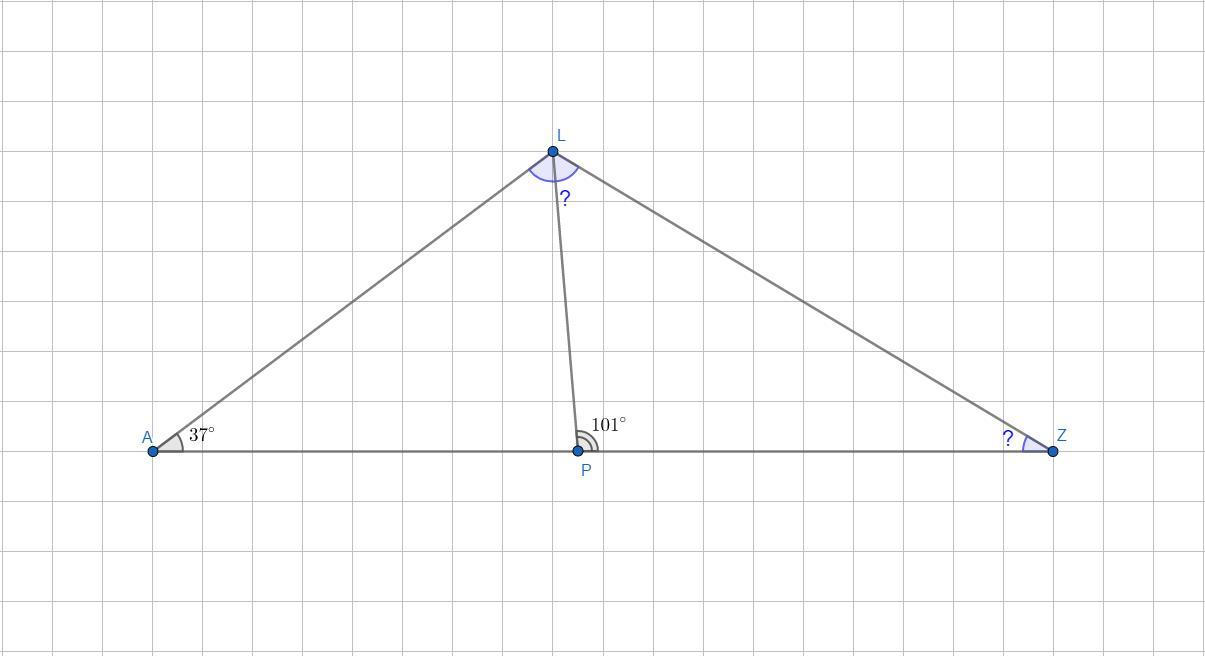
LP — биссектриса, проведённая в треугольнике ALZ. Найди градусную меру углов ALZ и LZA,
если ZLPZ = 101°, ZLAP = 37°.
Заполни пропуски числами.
ALZ =
LZA =
помогите умоляю
Ответы
Автор ответа:
4
Ответ:
- ∠ALZ=128°
- ∠LZA=15°
Объяснение:
- Сумма смежных углов равна 180°.
- Теорема у сумме углов треугольника: сумма углов треугольника равна 180°.
∠APL и ∠ZPL - смежные, значит, ∠APL+∠ZPL=180°, откуда ∠APL=180°-∠ZPL=180°-101°=79°.
В ΔALP из т. о сумме углов треугольника: ∠ALP=180°-∠APL-∠PAL=180°-79°-37°=64°.
- Биссектриса угла - луч, исходящий из вершины углы и делящий угол пополам.
Т.к. LP - биссектриса ∠ALZ, то ∠ALP=∠ZLP=64°, тогда ∠ALZ=∠ALP+∠ZLP=64°+64°=128°.
В ΔPLZ из т. о сумме углов треугольника: ∠LZA=180°-∠ZLP-∠ZPL=180°-64°-101°=15°.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Лдаиугвьфисшйбчрй
Предмет: Русский язык,
автор: Alice20071
Предмет: Русский язык,
автор: Alben74
Предмет: Алгебра,
автор: Fragz
Предмет: Русский язык,
автор: Аноним