Предмет: Алгебра,
автор: bt78g9dktq
Дробные рациональные уравнения
3х2–5x-2/2-х/=0
Приложения:
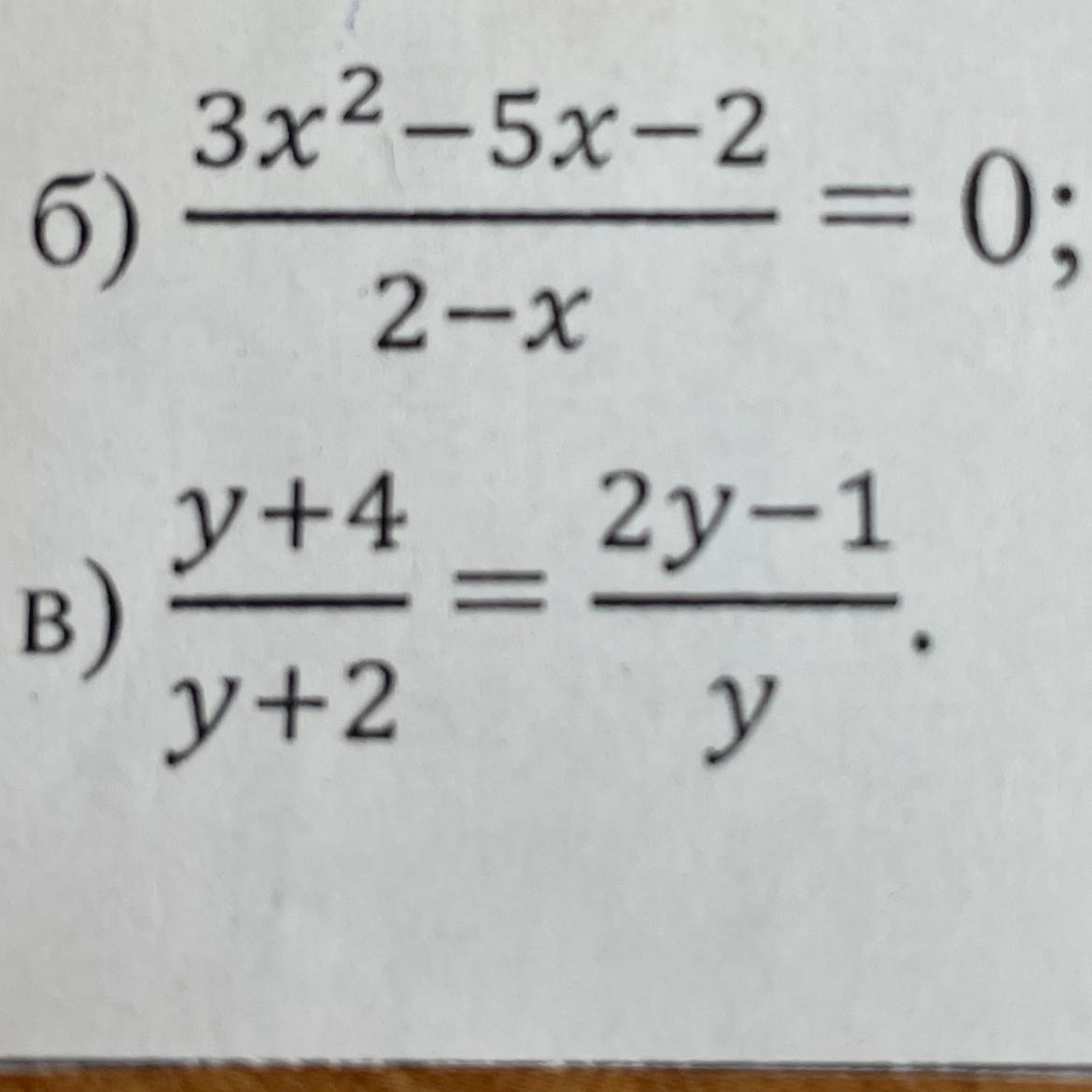
Ответы
Автор ответа:
0
Объяснение:
3x^2-5x-2=0
D=25+24=49
x1=(5+7)/6=2 не удовлетворяет области определения
x2=(5-7)/6=-1/3
(y+4)y=(2y-1)(y+2)
y²+4y=2y²-2+3y
y²-y-2=0
y1=2
y2=-1
Автор ответа:
0
Ответ:
Дробно-рациональные уравнения .
Отбрасываем корень х=2 , так как дробь не имеет смысла при этом значении переменной х .
Ответ: .
Похожие вопросы
Предмет: Другие предметы,
автор: АндрейТащер228
Предмет: Русский язык,
автор: NelfoRmalgu
Предмет: Другие предметы,
автор: ЕЕЕRОЦК0
Предмет: Химия,
автор: baron30
Предмет: Алгебра,
автор: gamesfor84