Предмет: Геометрия,
автор: ejjjjjkkiii
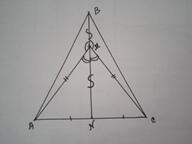
Задан треугольник ABC. Точка M лежит на медиане BN; AM = MC. Докажите, что AB = CB.
Ответы
Автор ответа:
1
Объяснение:
Дано: ΔАВС, BN - медиана, АМ=МС. Доказать: АВ=СВ.
ΔАМN=ΔCMN по третьему признаку (MN - общая сторона, АМ=СМ по условию, АN=CN по определению медианы),
Значит, ∠АМN=∠CMN.
ΔАВМ=ΔСВМ по первому признаку (∠АМВ=∠СМВ как смежные с углами АМN и CMN. ВМ = общая сторона, АМ=СМ по условию)
Из равенства треугольников следует, что АВ=СВ, доказано.
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: Ринаточк
Предмет: Русский язык,
автор: Yaraslavgetmacter
Предмет: Русский язык,
автор: Зебо11
Предмет: Математика,
автор: govnu4kavonu4ka
Предмет: Математика,
автор: danyasmoyalkov