Предмет: Алгебра,
автор: suvorova171177
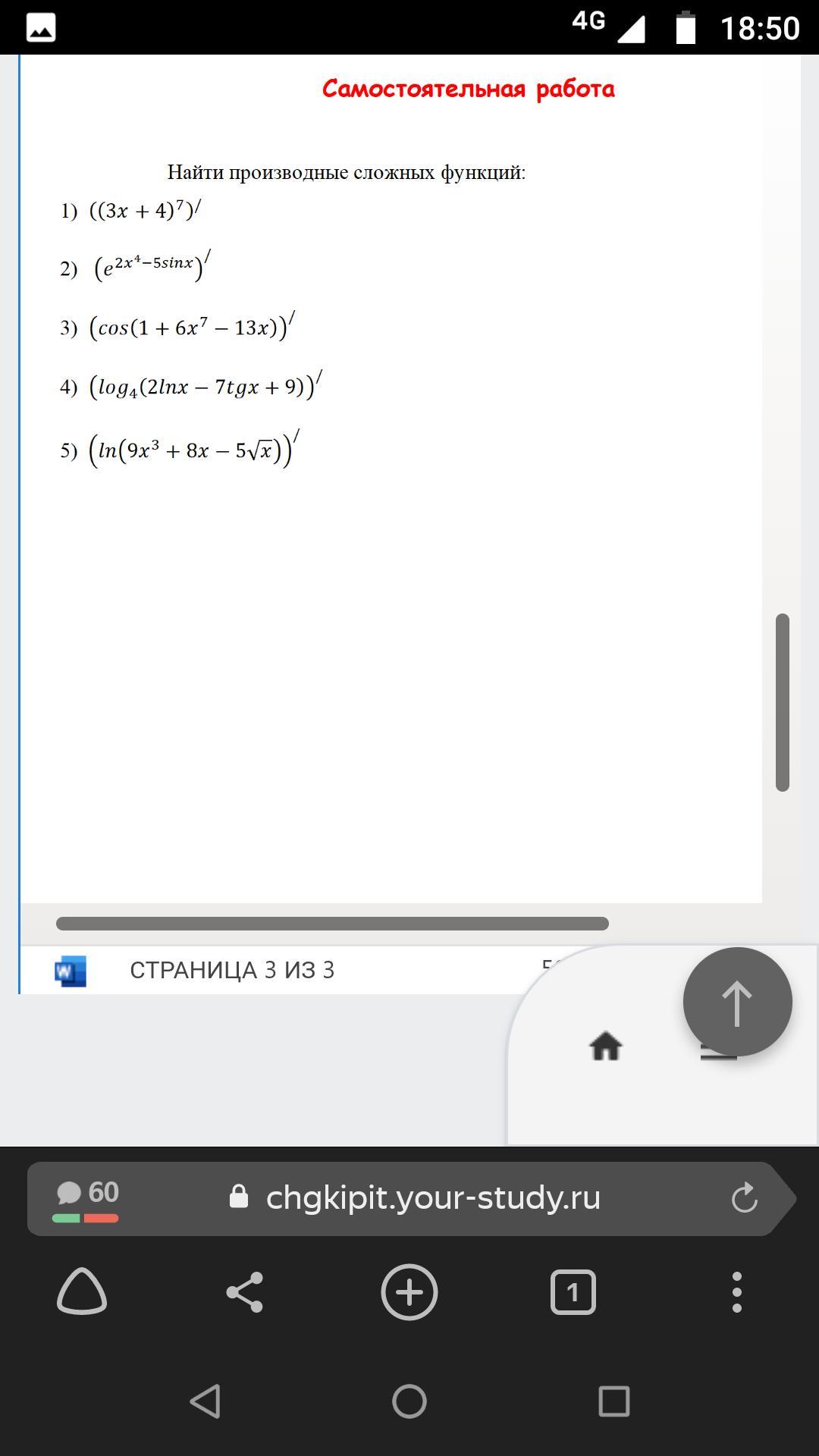
Помогите пожалуйста решить срочно.
Приложения:
Ответы
Автор ответа:
0
Ответ:
1)
2)
3)
4)
5)
Приложения:
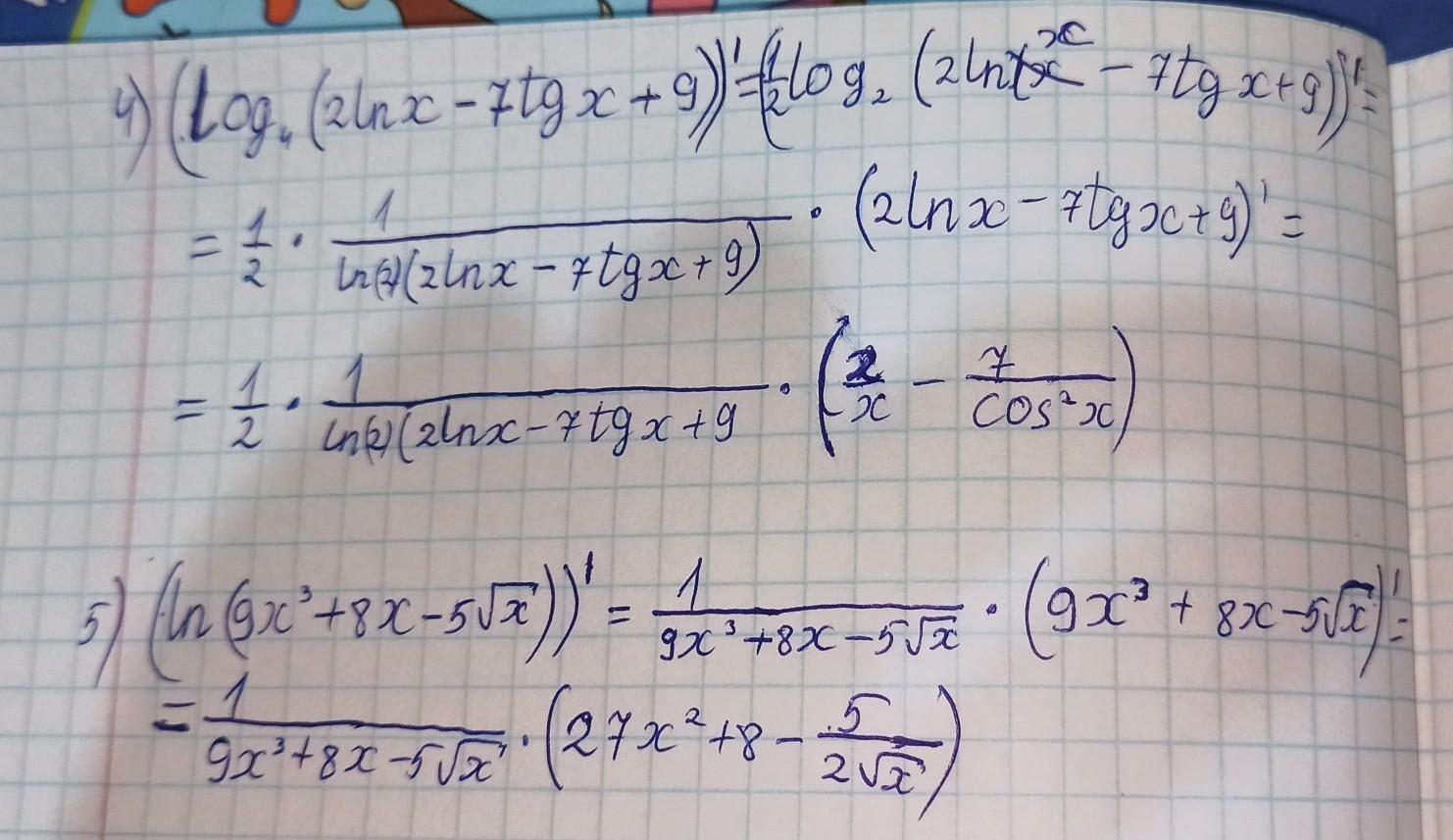
bertramjeratire:
Так там 4 и 5
4 не открыл
Открой пожалуйста.
4.
Зайди в фото, там и 4 есть, и 5
5 открылся а 4 нет .
Ну ничем помочь не могу
Открой пожалуйста 4 прошу тебя ?.
Как открою-то? Он не закрыт
Спасибо большое .
Похожие вопросы
Предмет: Русский язык,
автор: vlada181
Предмет: Қазақ тiлi,
автор: Sguseva41
Предмет: Русский язык,
автор: роза272
Предмет: Литература,
автор: polinasenchak06
Предмет: Русский язык,
автор: hayumisan