Question

можете помочь дам 50баллов но только честно​

Answer 1

Ответ:

Пошаговое объяснение:

Answer 2

Ответ:

В решении.

Пошаговое объяснение:

Решить систему неравенств:

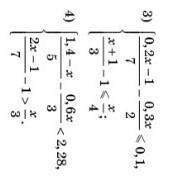
3) (0,2х - 1)/7 - 0,3х/2 <= 0,1

   (х + 1)/3 - 1 <= x/4

Умножить первое уравнение на 14, второе на 12, чтобы избавиться от дробного выражения:

2(0,2х - 1) - 7 * 0,3х <= 1,4

4(х + 1) - 12 <= 3х

Раскрыть скобки:

0,4х - 2 - 2,1х <= 1,4

4x + 4 - 12 <= 3x

Привести подобные:

-1,7x - 2 <= 1,4

4x - 8 <= 3x

-1,7x <= 1,4 + 2

4x - 3x <= 8

-1,7x <= 3,4

x <= 8

x >= 3,4/-1,7  знак неравенства меняется при делении на минус;

x <= 8

x >= -2;

x <= 8;

Решения первого неравенства: х∈[-2; +∞).

Решения второго неравенства: х∈(-∞; 8].

Неравенства нестрогие, скобки квадратные, а знаки бесконечности всегда под круглой скобкой.

Решения системы неравенств: х∈[-2; 8], пересечение.

4) (1,4 - х)/5 - 0,6х/3 < 2,28

    (2х - 1)/7 - 1 > х/3

Умножить первое уравнение на 15, второе на 21, чтобы избавиться от дробного выражения:

3(1,4 - х) - 5 * 0,6х < 34,2

3(2х - 1) - 21 > 7х

Раскрыть скобки:

4,2 - 3х - 3х < 34,2

6х - 3 - 21 > 7х

Привести подобные:

4,2 - 6х < 34,2

6х - 24 > 7х

-6х < 34,2 - 4,2

6х - 7х > 24

-6х < 30

-x > 24

x > 30/-6

x < 24/-1

x > -5;

x < -24;

Решения первого неравенства: х∈(-5; +∞).

Решения второго неравенства: х∈(-∞; -24).

Неравенства строгие, скобки круглые.

Системы неравенств не имеет решений.