Реши задачу.
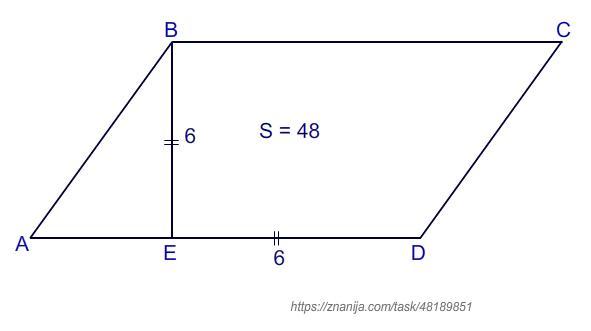
В параллелограмме ABCD: BE - Высота, BE = ED = 6. Площадь параллелограмма
ABCD равна 48. Найди длину АЕ.
Ответы
Ответ:
AE = 2.
Пошаговое объяснение:
Найти длину отрезка AE в параллелограмме ABCD, если известны его высота и площадь.
Дано:
ABCD - параллелограмм,
BE - высота,
BE = ED = 6,
S(ABCD) = 48.
Найти: AE.
Решение.
Рисунок прилагается.
Параллелограмм - это четырехугольник, в котором противолежащие стороны попарно параллельны.
Высота параллелограмма - это перпендикуляр, опущенный из вершины параллелограмма на противолежащую сторону.
Площадь параллелограмма равна произведению его основания на высоту: S = ah.
1) По условию задачи известна высота параллелограмма BE и его площадь.
BE - это высота параллелограмма, проведенная из вершины B к стороне AD.
Из формулы площади параллелограмма найдем сторону AD.
S(ABCD) = BE· AD;
AD = S(ABCD) / BE.
AD = 48 : 6 = 8.
AD = 8.
2) Найдем длину отрезка AE.
По условию BE = ED = 6.
Сторона параллелограмма AD состоит из отрезков AE и ED.
AD = AE + ED;
AE = AD - ED;
AE = 8 - 6 = 2.
Длина отрезка AE равна 2.