Предмет: Математика,
автор: sadsadsadasdsad1212
Найти решение задачи Коши
y'+2y/x=1/x^2, y(2)=1
Ответы
Автор ответа:
1
Ответ:
метод Эйлера
найдём μ(x)
теперь нужно умножить это уравнение на найденный множитель μ(x)=х²
теперь используем то что у(2)=1 чтобы найти С
теперь запишем ответ с известной константой
(решения методом Бернулли на фото)
Приложения:
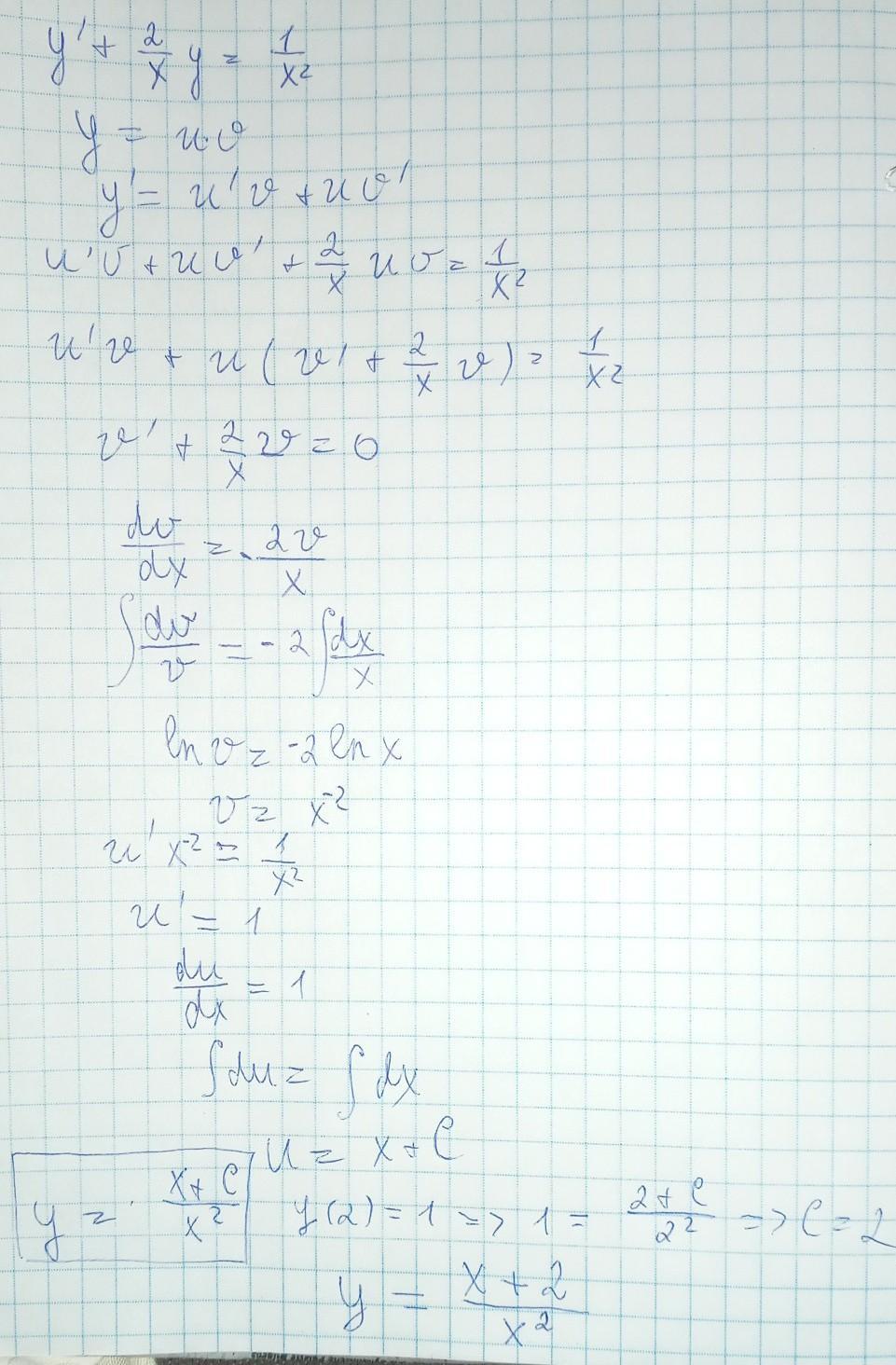
sadsadsadasdsad1212:
Надо методомy y=uv; y'=u'v+uv'
в условии не было сказано что нужно именно этим методом))) ну ладно щас исправлю
По фактам, мой косяк. Заранее спасибо
❤️
на фото тот метод о котором Вы говорили)☺
Похожие вопросы
Предмет: Окружающий мир,
автор: veronak1
Предмет: Беларуская мова,
автор: Аноним
Предмет: Другие предметы,
автор: Аноним
Предмет: Информатика,
автор: chipay
Предмет: Литература,
автор: vitalikivaniushka