Предмет: Алгебра,
автор: ElskerNorge
Найти промежутки монотонности и точки экстремума функции
а) y=x^4-2x^2-3
Ответы
Автор ответа:
5
Ответ:
Функция возрастает на промежутках [-1; 0]; [1; +∞);
Функция убывает на промежутках (-∞; -1]; [0; 1].
Точки экстремумов:
x min = -1; x min = 1;
x max = 0.
Пошаговое объяснение:
Требуется найти промежутки монотонности и точки экстремума функции.
- Для того, чтобы найти промежутки монотонности и точки экстремума функции, найдем производную первого порядка.
- Приравняем производную к нулю и найдем корни.
- Отметим их на числовой оси и найдем знаки производной на промежутках.
- Если производная положительна, то функция возрастает, если отрицательна - функция убывает.
- Если в точке производная меняет знак с плюса на минус, то в данной точке будет максимум, если с минуса на плюс - минимум.
1. у = х⁴ - 2х² - 3
Найдем производную:
y' = 4x³ - 2 · 2x = 4x³ - 4x = 4x(x² - 1) = 4x(x - 1)(x + 1)
Приравняем к нулю и найдем корни:
4x(x - 1)(x + 1) = 0
х = 0; х = 1; х = -1.
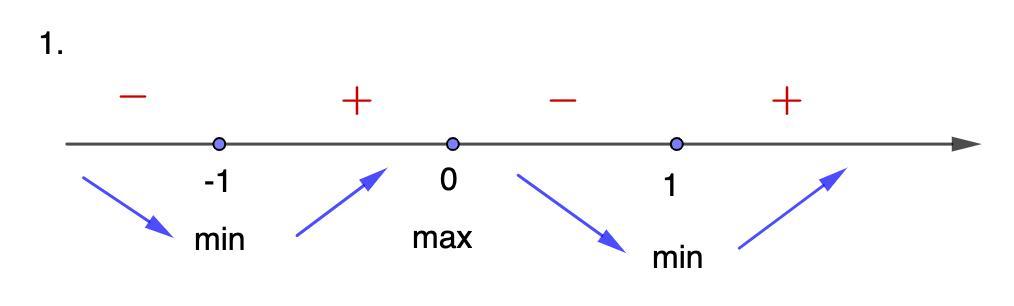
Отметим эти точки на числовой оси и определим знаки производной на промежутках.
См. рисунок.
Функция возрастает на промежутках [-1; 0]; [1; +∞);
Функция убывает на промежутках (-∞; -1]; [0; 1].
Точки экстремумов:
x min = -1; x min = 1;
x max = 0.
Приложения:
Похожие вопросы
Предмет: Українська мова,
автор: ipayuhimyuk
Предмет: Беларуская мова,
автор: Iiz
Предмет: Қазақ тiлi,
автор: амир20081
Предмет: Русский язык,
автор: zool29
Предмет: Алгебра,
автор: solasharel844