Предмет: Алгебра,
автор: Аноним
❗‼️❗❗❗❗❗❗❗❗❗❗❗❗
пожалуйста Только без любителей бесплатных баллов.
буду банить!!!!!!
все на фото
хотя бы одно.
не понимаю как это решить❗
Приложения:
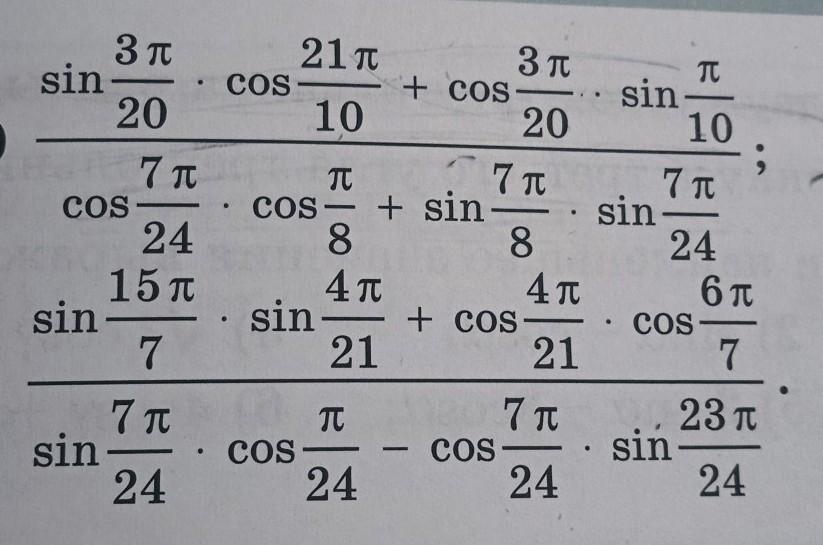
Ответы
Автор ответа:
2
Ответ:
Пользуемся формулами приведения , формулами суммы и разности тригонометрических функций .
Значения , тогда в результате
получим .
Аноним:
спосибо вам! я думал уже не кто не ответить, Спосибооо ещё раз.
пожалуйста, просто долго писать в редакторе формул
а можно пожалуйста поинтересоваться?
А нет, все. понял. Спасибо ещё раз...
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: awaisman228
Предмет: Английский язык,
автор: серж220
Предмет: Українська мова,
автор: Аноним
Предмет: Музыка,
автор: Kotya44