Question

Помогите, пожалуйста с решением этой задачи

Answer 1

Ответ:

20005

Пошаговое объяснение:

Пусть в этих 440 числах

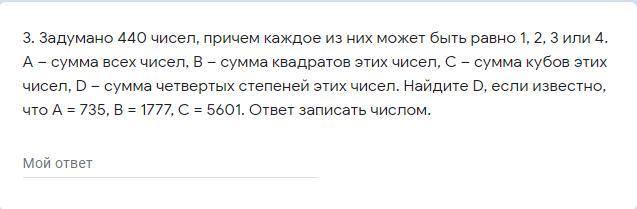
чисел 1 - n штук, чисел 2 - k штук, чисел 3 - m штук, чисел 4 - s штук, где n, k, m, s ∈ N, и не одно из них не равно 0 (по условию), тогда можно записать:

n+k+m+s=440; - всего чисел 440

n+2k+3m+4s=735; - сумма чисел

n*1²+k*2²+m*3²+s*4²=1777; - сумма квадратов чисел

n+k2³+m3³+s4³=5601; - сумма кубов чисел.

Получаем систему из 4-х линейных уравнений относительно n, k, m, s.

Система линейных уравнений решается одним из многих известных способов.

Составим матрицу:

1  1   1      1  440

1  2  3    4  735

1  4  9  16  1777

1  8 27 64 5601

Применив метод Крамера (посчитав все необходимые определители 4-ого порядка). Ну, считаем не "вручную", а на компе. Например в EXCEL-е. Получилм:

n=307;

k=35;

m=34;

s=64.

Ну и последнее действие: найдем сумму 4-х степепей:

1*307+35*2⁴+34*3⁴+64*4⁴=20005