Question

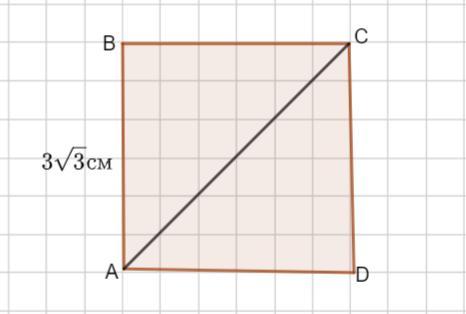
в квадрате abcd сторона ab =3 корня из 3 см. найди диагональ квадрата ac​

Answer 1

Ответ:

Диагональ квадрата АС = 3√6 см.

Объяснение:

Пусть дан квадрат АВСD   АВ= 3√3 см.

Найдем диагональ квадрата по формуле

$d= a\sqrt{2}$,  a- сторона квадрата

Тогда диагональ будет

$d= 3\sqrt{3} \cdot\sqrt{2} =3\sqrt{6}$  см

Или же можно по другому. Диагональ квадрата делит его на два прямоугольных треугольника. Применим теорему Пифагора к одному из них

Теорема Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов

Δ АВС - прямоугольный.

$AC^{2} =AB^{2} +BC^{2} ;\\AC= \sqrt{AB^{2} +BC^{2}} ;\\AC= \sqrt{(3\sqrt{3} )^{2} +(3\sqrt{3} )^{2} } =\sqrt{27+27} =\sqrt{54} =\sqrt{9\cdot6} =3\sqrt{6}$  

Диагональ квадрата АС = 3√6 см.