Question

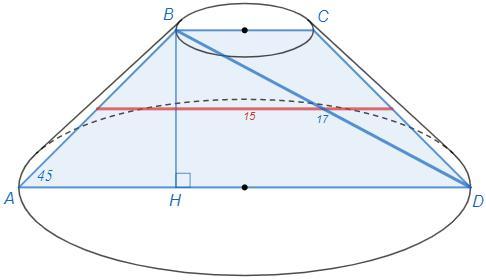
Осевое сечение усечённого конуса - равнобедренная трапеция, острый угол который равен 45°, диагональ - 17см и средняя линия - 15 см . Найдите площадь боковой поверхности усеченного конуса​

Answer 1

В сантиметрах

Площадь боковой поверхности усеченного конуса​

S_бок = п (r+r1) L

r=AD/2, r1=BC/2

r+r1 =(AD+BC)/2 =15 (средняя линия трапеции)

Найдем L=AB. Опустим высоту BH. В равнобедренной трапеции отрезок HD равен средней линии, 15.

BH=√(BD^2-HD^2) =√(17^2-15^2) =8 (т Пифагора)

AB =BH/sin45 =8√2

S_бок =п *15 *8√2 =120√2 п  ~533,15 (см^2)