обязательная часть 1) Найдите углы при основании равнобедренного треугольника, если угол между его боковыми сторонами а Б равен 70°. 2); Параллельные прямые аи ба пересечены прямой с (рис. 7). Из вестно, что 21 = 150°. Определитет YT Рис. 7 угол 2. Дополнительная часть 3) Докажите, что точка D, лежащая на биссектрисе угла В, находится на одинаковом расстоянии от сторон угла.

Ответы
Ответ:
СМ НИЖЕ
Объяснение:
1) У равнобедренного треугольника углы при основании равны ⇒ 180°-70° =110°:2=55°
2) ∠3=∠2 как вертикальные углы по построению
∠3+∠1=180° как внутренние односторонние при a║b
∠3=180-∠1=180°-150°=30° ⇒∠3=∠2=30°
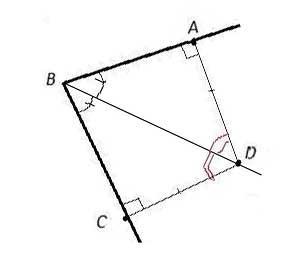
3) Расстояние от точки D (на биссектрисе) до стороны угла измеряется длиной перпендикуляра, опущенного из этой точки на сторону угла.
∠DАB=∠DCВ=90°
∠АBD=∠CBD, так как BD- биссектриса ∠.
Соответственно, ∠АDB=90°-∠АBD и ∠ВDC=90°-∠CBD - как острые углы прямоугольного Δ⇒
Следовательно, что ∠АDB=∠ВDC
По второму признаку равенства Δ: сторона и два прилежащих к ней угла одного = соответственно стороне и 2 углам другого ⇒ BD - общая, ∠АDB=∠ВDC и ∠АBD=∠CBD ⇒ ΔАBD=ΔCBD.
В равных Δ против соответственно равных углов лежат равные стороны, отсюда AD=CD, что и требовалось доказать