ПОМОГИТЕ ПОЖАЛУЙСТА СРОЧНО!!! Нужно написать ДАНО ко ВСЕМ задачам ! Я НЕ ЗНАЮ КАК ИМЕННО ЭТО ЗАПИСАТЬ! ЭТО ВООБЩЕ ИЗ УРОВНЯ 10-ГО КЛАССА, (ИМЕННО КАК НУЖНО РАСПИСАТЬ),НО Я В 8-ОМ! ПОМОГИТЕ УМОЛЯЮ!!! ДАМ 100 БАЛЛОВ ТОЛЬКО СДЕЛАЙТЕ ПРОШУ!!!! РЕШЕНИЕ УЖЕ САМА ПОПРОБУЮ НАПИСАТЬ!
1. Вистота рівнобедреного трикутника, проведена до основи, дорівнює 5 см, а довжина основи 24 см. Знайдіть синус, косинус, тангенс і котангенс кута при основі трикутника. 2. Розв'яжіть прямокутний трикутник за катетом і гострим кутом а) а = 2 β = 45°; б) а = 4, а = 18. 3. розв'яжіть прямокутний трикутник за гіпотенузою і катетом: а) с = 9√2, а = 9; б) с = 25, а = 24
Ответы
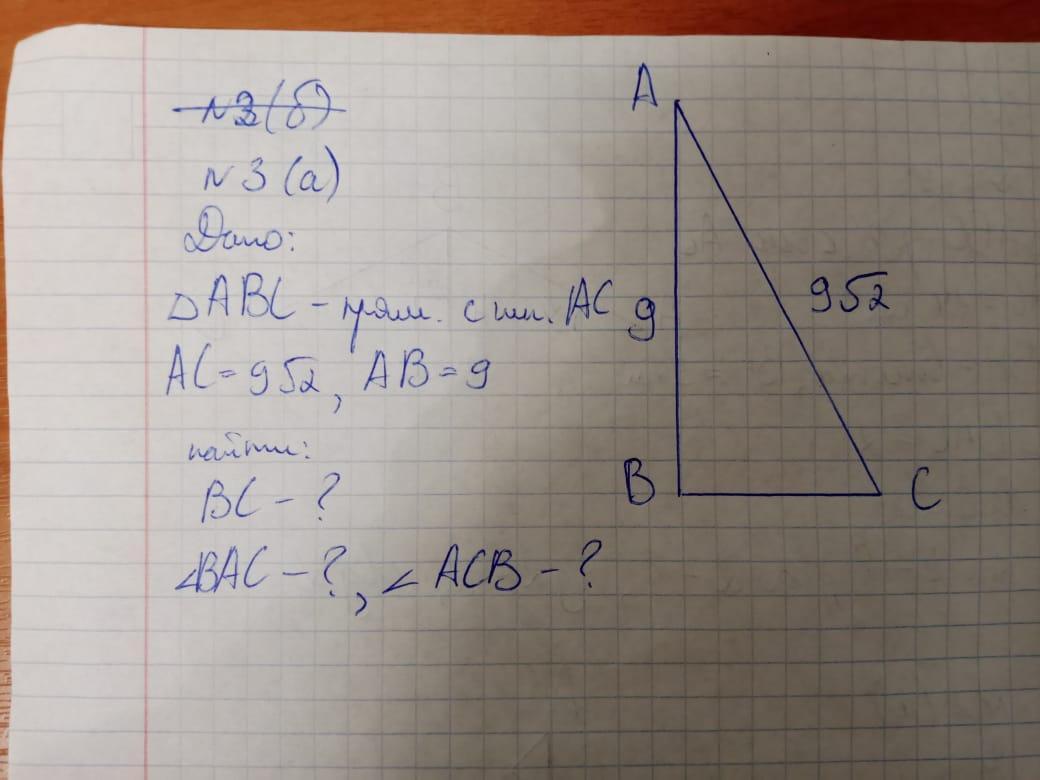
См. фото
Во вторых пунктах заданий 2 и 3 изменятся только значения:
во 2(б) - AB = 4, β = 18°
(и два варианта решения - в зависимости от расположения угла относительно катета)
в 3(б) - AC = 25, AB = 24
ред.
исходя из того, что в пункте а второго номера углы кроме прямого будут равны, то на их расположении внимание заострять не стоит
но в пункте б возможны вариации: углом альфа будет выступать или BAC, или ACB, в этом случае нужно два чертежа и два разных решения
формулы для поиска сторон треугольника по острому углу и катету: https://www.fxyz.ru/%D1%84%D0%BE%D1%80%D0%BC%D1%83%D0%BB%D1%8B_%D0%BF%D0%BE_%D0%B3%D0%B5%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D0%B8/%D0%BF%D0%BB%D0%BE%D1%81%D0%BA%D0%B8%D0%B5_%D1%84%D0%B8%D0%B3%D1%83%D1%80%D1%8B/%D1%82%D1%80%D0%B5%D1%83%D0%B3%D0%BE%D0%BB%D1%8C%D0%BD%D0%B8%D0%BA/%D1%80%D0%B5%D1%88%D0%B5%D0%BD%D0%B8%D0%B5_%D0%BF%D1%80%D1%8F%D0%BC%D0%BE%D1%83%D0%B3%D0%BE%D0%BB%D1%8C%D0%BD%D0%BE%D0%B3%D0%BE_%D1%82%D1%80%D0%B5%D1%83%D0%B3%D0%BE%D0%BB%D1%8C%D0%BD%D0%B8%D0%BA%D0%B0/
(внизу страницы)
второй угол ищется как 90° - первый угол
рекомендации к решению:
1 - найти половину AC, решить треугольник ABH, через соотношения сторон этого треугольника найти искомое
3 - по т. Пифагора a) р/б треугольник, стороны равны, углы по 45
б) третья сторона - 7(возможны ошибки), углы можно найти через соотношения сторон(вернее, найти синусы, косинусы, ... углов, а через них сами углы)