Предмет: Геометрия,
автор: avika5697
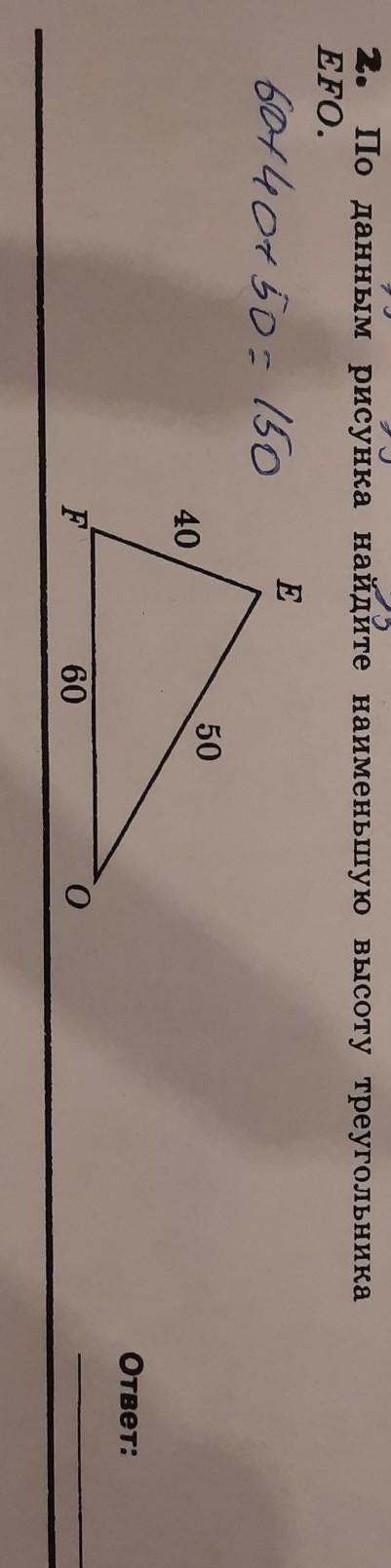
ГЕОМЕТРИЯ.ПЛОЩАДЬ ТРЕУГОЛЬНИКА. по данным рисунка найдите наименьшую высоту треугольника EFO
Приложения:
Ответы
Автор ответа:
1
Вычислим площадь треугольника по формуле Герона:
Далее, площадь треугольника может быть вычислена как половина произведения основания на высоту. Чтобы высота была наименьшей, сторону нужно выбрать наибольшую:
Ответ получен.
Мы пользовались такими обозначениями: a=60, b=50, c=40 - стороны треугольника; p=(a+b+c)/2 =75 - полупериметр треугольника; h - высота, опущенная на сторону a.
Похожие вопросы
Предмет: Английский язык,
автор: номер22
Предмет: Английский язык,
автор: Аноним
Предмет: Русский язык,
автор: Пацанчик26
Предмет: Математика,
автор: stella20081
Предмет: Математика,
автор: KatyaDaki