Предмет: Алгебра,
автор: v1234566789
Помогите пожалуйста!!
Спростити вираз \frac{{a - 64}}{{\sqrt a + 3}}\cdot\frac{1}{{a + 8\sqrt a }} - \frac{{\sqrt a + 8}}{{a - 3\sqrt a }}
Знайдіть його значення якщо a = 3.
С подробным решением пожалуйста!
Приложения:

Ответы
Автор ответа:
8
Ответ:
Объяснение:
!!!!!!!!!!!!!!!!!!!!!!!!!!!
Приложения:
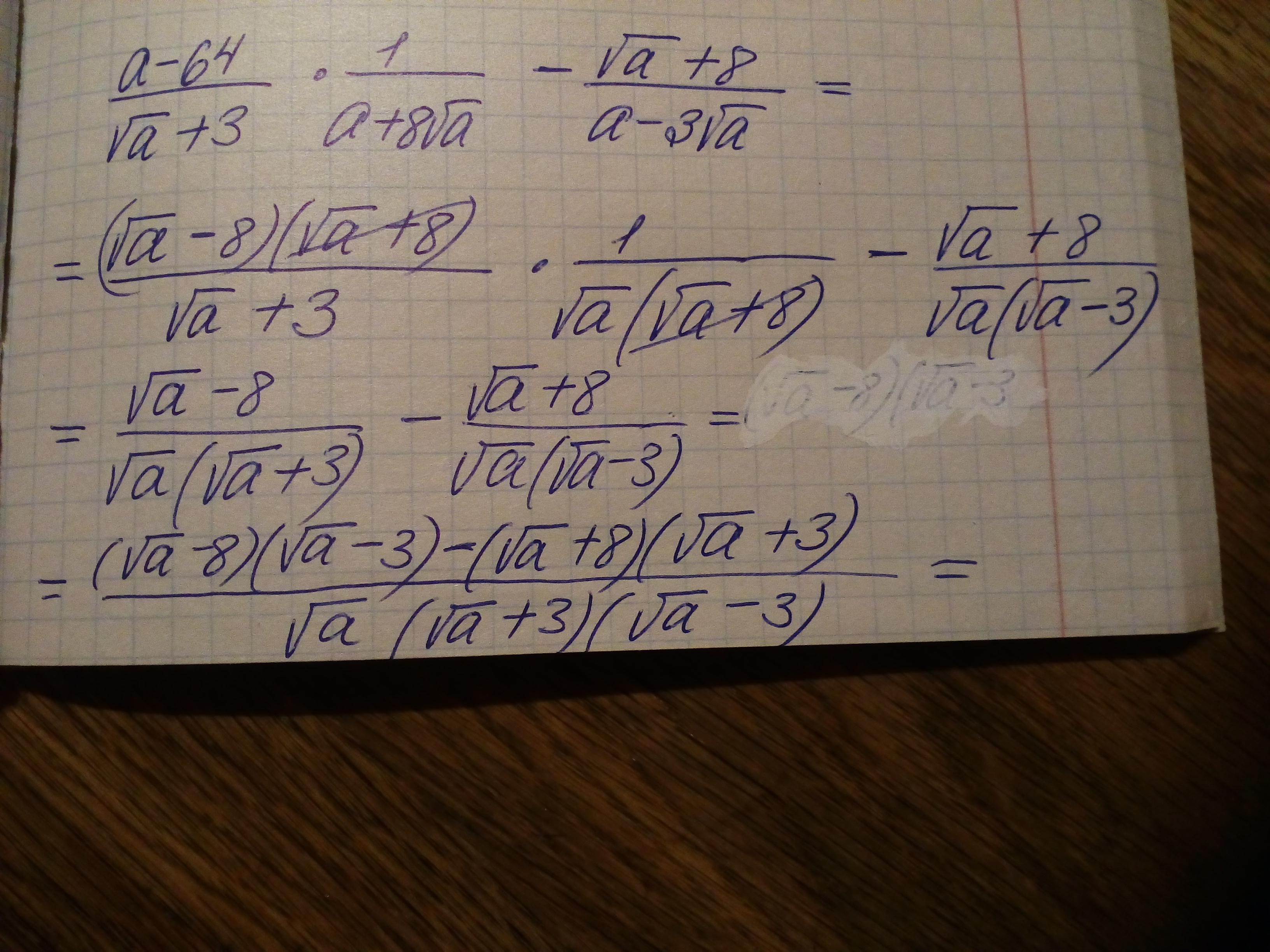
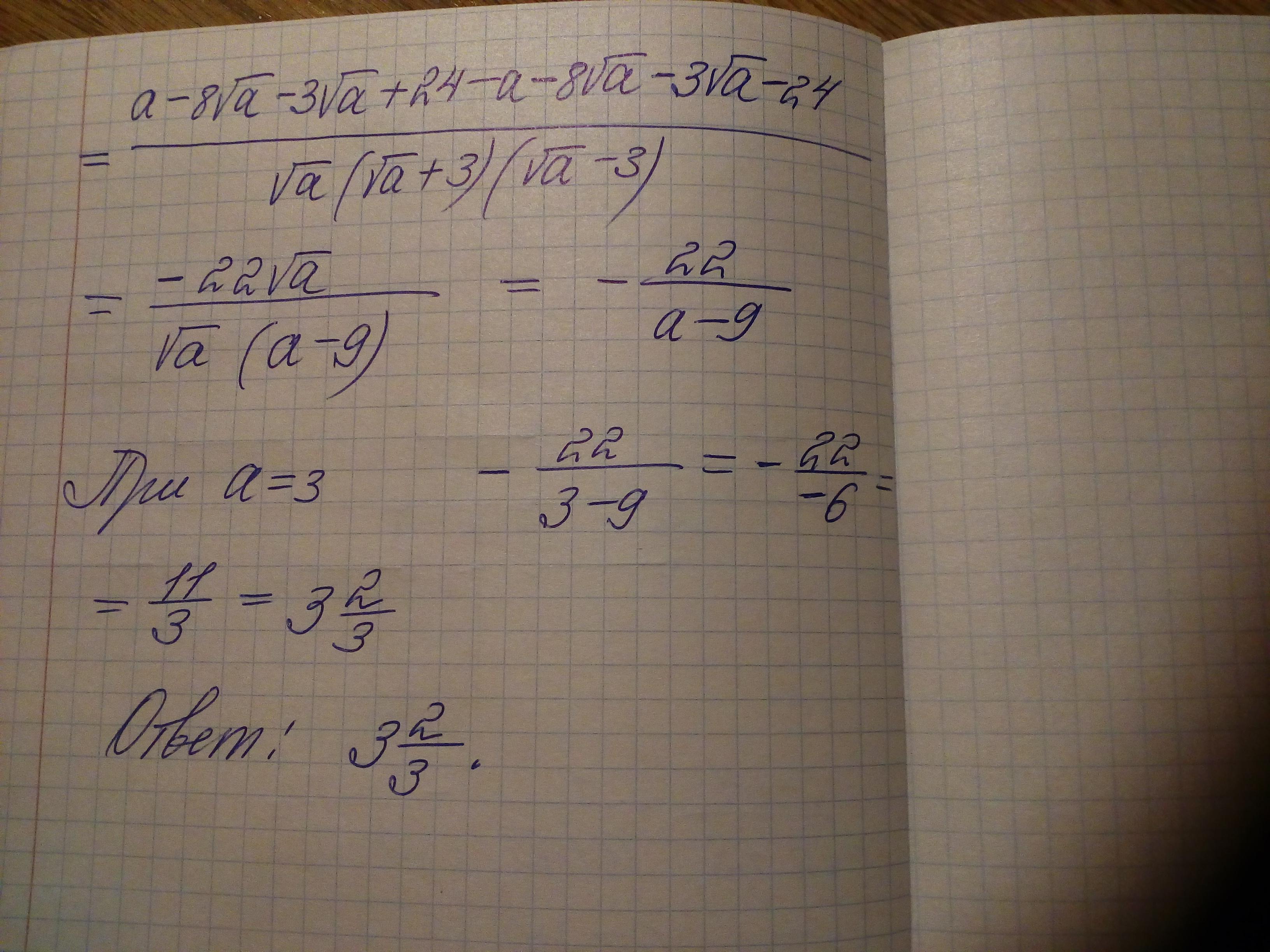
myklasofia:
ДЯКУЮ!!! ЧИМ ПОБІЛЬШЕ ТАКИХ ЛЮДЕЙ!!!!!
Автор ответа:
10
a=3 ⇒
Что у тебя за почерек просто ужас
это не мойпочерк
это вообще школа?
рог
это правильно
a+8
a
1
−
a−3
a
a
+8
=
\displaystyle =\frac{{(\sqrt{a} - 8)(\sqrt{a} +8)}}{{\sqrt a + 3}}*\frac{1}{\sqrt{a} (\sqrt{a} +8)} - \frac{{\sqrt a + 8}}{{a - 3\sqrt a }}==
a
+3
(
a
−8)(
a
+8)
∗
a
(
a
+8)
1
−
a−3
a
a
+8
=
\displaystyle =\frac{{(\sqrt{a} - 8)}}{{\sqrt a + 3}}*\frac{1}{\sqrt{a} } - \frac{{\sqrt a + 8}}{{\sqrt{a}(\sqrt{a} - 3) }}==
a
+3
(
a
−8)
∗
a
1
−
a
(
a
−3)
a
+8
a
1
−
a−3
a
a
+8
=
\displaystyle =\frac{{(\sqrt{a} - 8)(\sqrt{a} +8)}}{{\sqrt a + 3}}*\frac{1}{\sqrt{a} (\sqrt{a} +8)} - \frac{{\sqrt a + 8}}{{a - 3\sqrt a }}==
a
+3
(
a
−8)(
a
+8)
∗
a
(
a
+8)
1
−
a−3
a
a
+8
=
\displaystyle =\frac{{(\sqrt{a} - 8)}}{{\sqrt a + 3}}*\frac{1}{\sqrt{a} } - \frac{{\sqrt a + 8}}{{\sqrt{a}(\sqrt{a} - 3) }}==
a
+3
(
a
−8)
∗
a
1
−
a
(
a
−3)
a
+8
Похожие вопросы
Предмет: Русский язык,
автор: аружан139
Предмет: Русский язык,
автор: ленок158
Предмет: Русский язык,
автор: IgorekLeonLeonov
Предмет: Английский язык,
автор: ak1989se
Предмет: Алгебра,
автор: p0larbear