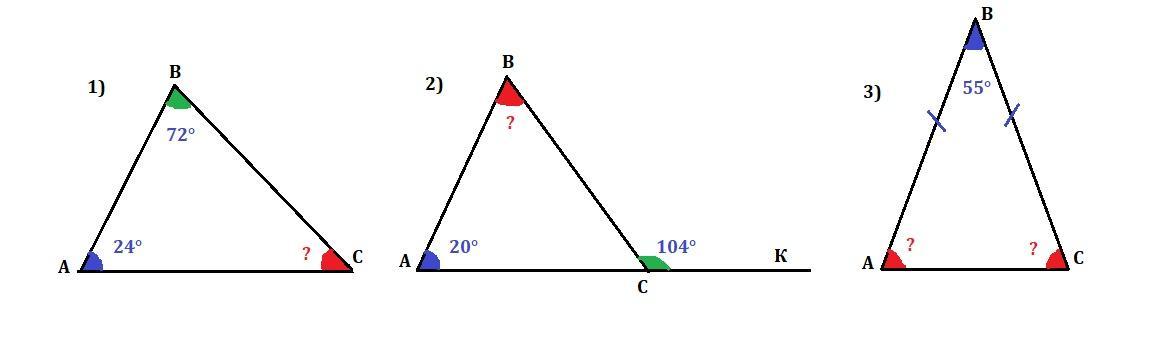
1. Найдите угол C треугольника ABC, если угол A = 24°, угол B = 72. Определить вид треугольника.
2. Внешний угол треугольника равен 104°, а внутренний угол, не смежный с ним, равен 20°. Найти неизвестные углы треугольника.
3. Найти углы равнобедренного треугольника, если угол, противоположный основанию равен 55°.

Ответы
Ответ:
1) ∠С=84°, ΔАВС - остроугольный.
2)∠В=84°
3)∠А=∠С=62,5°
Объяснение:
1. Найдите угол C треугольника ABC, если угол A = 24°, угол B = 72. Определить вид треугольника.
Сумма углов треугольника равна 180°. Поэтому
∠С=180°-∠А-∠В=180°-24°-72°=84°.
Если все углы треугольника меньше 90°, то такой треугольник называется остроугольным.
2. Внешний угол треугольника равен 104°, а внутренний угол, не смежный с ним, равен 20°. Найти неизвестные углы треугольника.
Внешний угол треугольника – это угол, смежный с любым из внутренних углов треугольника.
∠ВСК и ∠АСВ - смежные углы. ∠АСВ - внутренний угол ΔАВС. ⇒ ∠ВСК - внешний угол. ∠ВСК=104°
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
∠ВСК = ∠А+∠В. ∠А=20°, ⇒
∠В=∠ВСК-∠А=104°-20°=84°
3. Найти углы равнобедренного треугольника, если угол, противоположный основанию равен 55°.
Равнобедренный треугольник — треугольник, в котором две стороны равны между собой по длине. Боковыми называются равные стороны, а последняя неравная им сторона — основанием.
ΔАВС-равнобедренный. АВ=ВС. АС - основание. ∠В=55°
В равнобедренном треугольнике углы при основании равны.
∠А=∠С=(180°-∠В)÷2 = (180°-55°)÷2=125°÷2=62,5°