Question

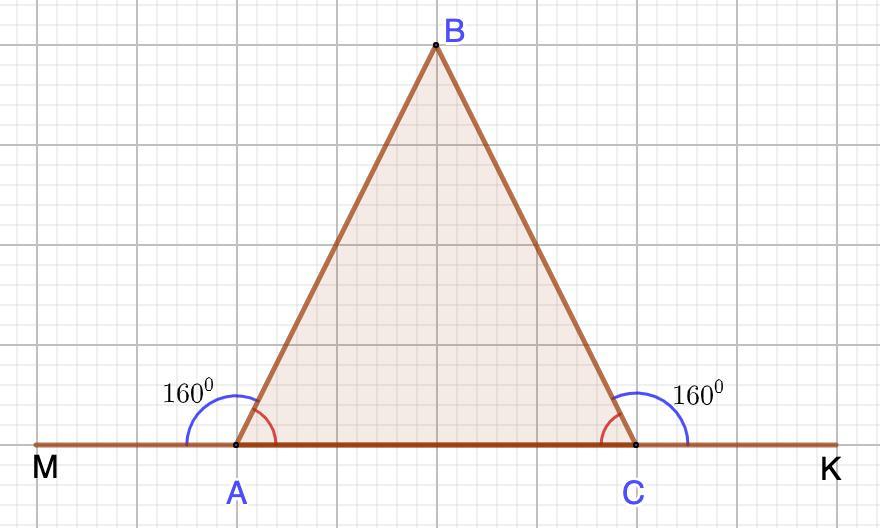
Найдите углы треугольника, если внешние углы при двух вершинах равна по 160∘.
Помогите срочно даю 20 баллов
​

Answer 1

Ответ:

20°, 20°, 140° - углы треугольника

Объяснение:

Пусть дан треугольник Δ АВС . По условию внешние углы при двух вершинах равны 160°. Тогда ∠ МАВ =∠ MCD =160°.

Угол, смежный с внутренним углом треугольника, называется внешним углом треугольника. Так как сумма смежных углов равна 180°, то  ∠ А=∠С =180°-160°=20°.

Сумма углов треугольника равна 180 °.

Тогда ∠В= 180°-(20°+20°)= 180°-40°=140°.

Answer 2

Ответ:

Углы треугольника АВС: ∠ВАС = 20°; ∠ВСА = 20°; ∠АВС = 140°.

Объяснение:

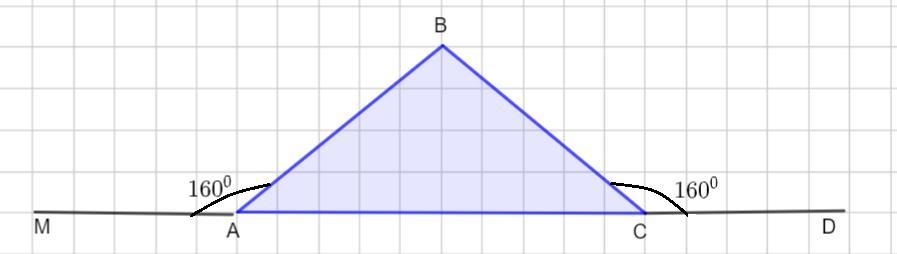
Требуется найти углы треугольника, если внешние углы при двух вершинах равна по 160°.

Дано: ΔАВС;

∠МАВ = ∠КСВ = 160° - внешние.

Найти: углы ΔАВС.

Решение:

• Сумма смежных углов равна 180°.

⇒ ∠ВАС = 180° - ∠МАВ = 180° - 160° = 20° (смежные);

∠ВСА = 180° - ∠КСВ = 180° - 160° = 20° (смежные).

• Сумма углов треугольника равна 180°.

∠АВС = 180° - ∠ВАС - ∠ВСА = 180° - 20° - 20° = 140°

Нашли углы треугольника АВС: ∠ВАС = 20°; ∠ВСА = 20°; ∠АВС = 140°.