ГЕОМЕТРИЯ 10 КЛАСС, ПОМОГИТЕ ПОЖАЛУЙСТА!!!
Если выбрать 4 случайные точки на сфере которые образуют вершины тетраидра, какова вероятность что центр сферы окажется внутри полученной фигуры.
Ответы
Ответ: 1/8
Пошаговое объяснение:
Чтобы найти вероятность выбрать на сфере 4 точки, чтобы центр окружности лежал внутри тетраэдра образованного этими точками, нужно найти вероятность, что каждая из 4-x выбранных последовательных точек имеет верное положение.
Вероятность того, что первая точка будет выбрана правильно равна 1. После выбора первой точки будем смотреть на сферу вдоль луча соединяющего центр сферы и данную точку (смотрим на соответствующую проекцию в виде окружности)
При выборе оставшихся трех точек возможны 3 случая:
1) Проекции трех оставшихся точек вместе с проекцией кругового сечения,(оно может быть эллипсом) в которое они вписаны образуют такой треугольник, что проекция центра сферы и первой точки (они сливаются при такой точке обзора) будет снаружи данного треугольника.
В данном случае центр сферы гарантированно не попадет внутрь тетраэдра.
2) Проекции трех оставшихся точек вместе с проекцией сферы образуют такой треугольник, что проекция центра сферы и первой точки (они сливаются при такой точке обзора) будет внутри данного треугольника, а также все данные точки будут лежат в противоположном полушаре от первой точки. За плоскость деления шара считаем диаметральное сечение перпендикулярное лучу обзора.(луч проходящий через первую точку и центр шара). В этом случае центр сферы попадает внутрь тетраэдра. (Рисунок 1)
3) Аналогично как случай 2, но оставшиеся 3 точки находятся в том же полушаре, что и первая точка. В этом случае центр сферы НЕ попадает внутрь тетраэдра.
Количество положений точек в случае 3 равно числу положений точек в случае 2 из-за симметрии.
Таким образом, вероятность попадания центра сферы внутрь вписанного в нее тетраэдра вдвое меньше чем вероятность попадания точки пересечения осей эллипса во вписанный в нее треугольник, что при рассмотрении наклона данной плоскости равносильно задаче попадания центра окружности во вписанный треугольник. То есть если точка лежит внутри плоской фигуры, то она будет лежат и внутри проекции этой плоской фигуры. (Рисунок 2)
Таким образом, мы ловко свели 3-d задачу к ее 2-d аналогу.
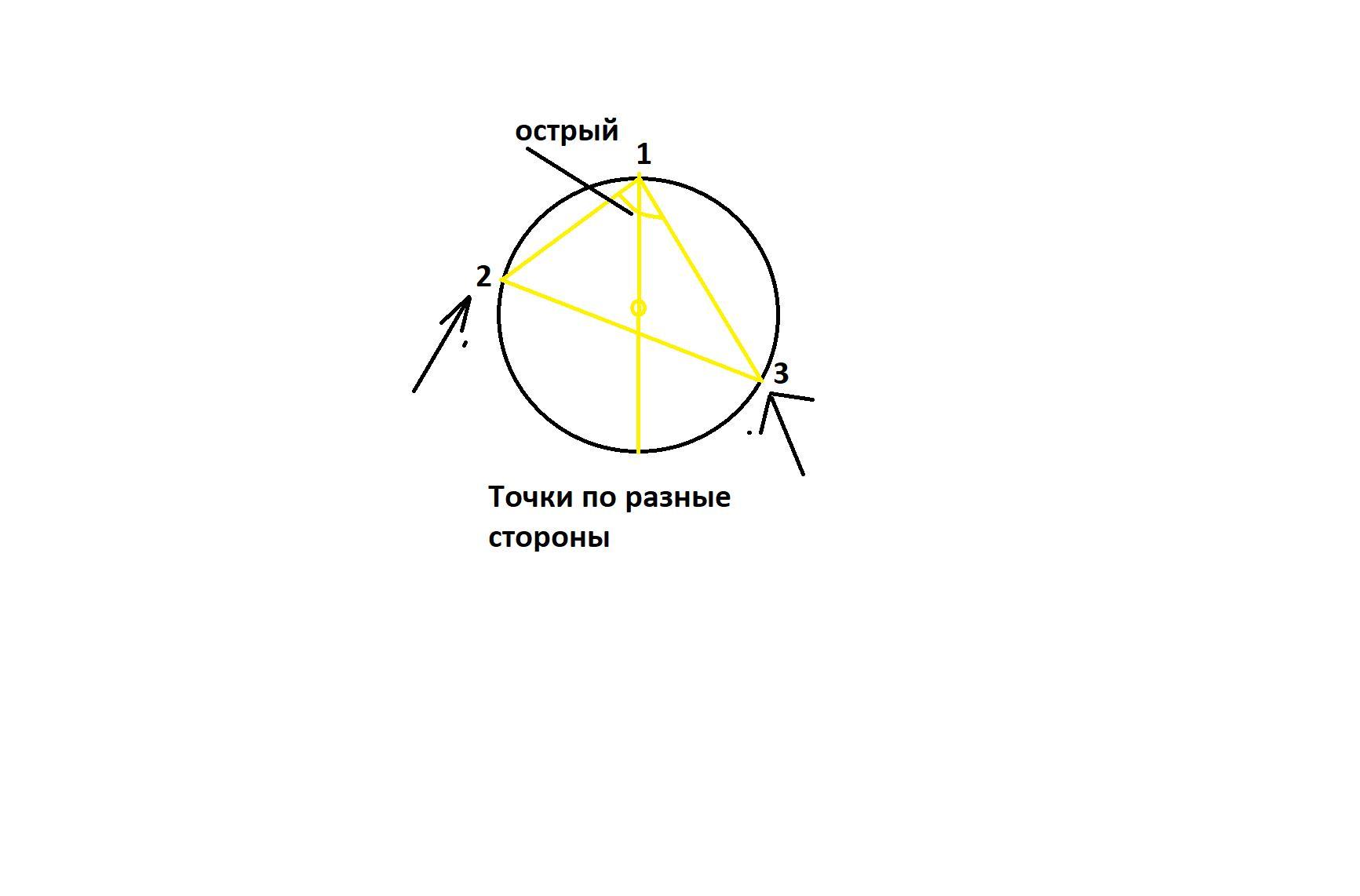
Для того, чтобы центр окружности был внутри вписанного треугольника, достаточно, чтобы он был остроугольным.
Проведем луч соединяющий одну из вершин и центр окружности, поделив окружность на два круга, тогда остроугольность будет достигнута при 2-x условиях.
1) Другие две точки лежат в разных полукругах.
2) Угол при первой вершине будет острым.
Вероятность первого условия равна сумме вероятностей, что вторая точка находится в первой полукруге, а третья во втором и наоборот, то есть: p1 = 1/2*1/2 + 1/2*1/2 = 1/2
Вероятность второго события: p2 = 90/180 = 1/2.
Таким образом вероятность того, что центр окружности попадет во вписанный треугольник равна: p3 = 1/2 * 1/2 = 1/4.
Из сказанного выше, вероятность попадания центра сферы во вписанный в нее тетраэдр:
P = p3/2 = 1/8