Помогите умоляю пожалуйста.
Ответы
Ответ:
Объяснение:
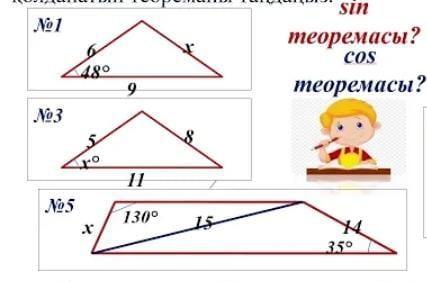
1) Дано: ΔABC, c=6, b=9, α=48°. Найти х
Решение: по теореме косинусов: Квадрат стороны треугольника равен сумме квадратов двух других сторон за вычетом удвоенного произведения этих сторон на косинус угла между ними. ⇒х²=b²+c²-2bc·Cos 48°=6²+9²-2·6·9·Cos48°≈36+81-108·0,6691=117-72,2628=44,7372
⇒x=√44,7372=6,69
Ответ: х≈6,69
3) Дано: ΔABC, c=5, b=11, a=8. Найти х°
Решение:: по теореме косинусов:
Cosx= (b²+c²-a²)/(2bc)=(5²+11²-8²)/(2·5·11)= (25+121-64)/110=82/110=0,7455
Cosx= 0,7455 ⇒ x=41°35'≈42°
Ответ: х≈42°
5)Трапеция разделена диагональю на два треугольника.
1) Из правого треугольника по теореме синусов имеем:
15/Sin 35° - 14/Sinα, ⇒Sinα= 14·Sin36°/15 = 14·0,5736/15=0,5354
2) Из левого треугольника: 15/Sin130°= x/Sinβ ⇒ x= 15·Sinβ/Sin130°
но α=β как накрест лежащие углы при параллельных основаниях трапеции и секущей (диагональю)⇒Sinβ=Sinα=0,5354
Sin 130°=Sin 50°=0,766 ⇒x=15·0,766/0,5354=11,49/0,6354≈21,5
Ответ: х-21,5≈22