Предмет: Алгебра,
автор: danialalimbekov
ciga? 659. Упростите выражение: cos(-a) cos(180" + a). sin(-a) sin (90° + a) sin(-a) ctg(-a) 6) cos (360°-a). tg(180° + a) a) B) tg(180' - a) sin(210* + a) cos(180°-a) te(210-a)' cos(270° + a) etg(270'-a) sin (180 - 0) 18(270' + a) r) Только в и г
Приложения:
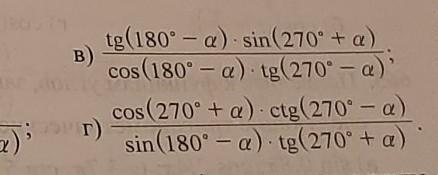
Ответы
Автор ответа:
3
в)
г)
Похожие вопросы
Предмет: Қазақ тiлi,
автор: 19019
Предмет: Английский язык,
автор: olgacrasivaja
Предмет: Английский язык,
автор: Neznayka1228
Предмет: Математика,
автор: serdolia
Предмет: Английский язык,
автор: paulokualo1922pelc1f