Question

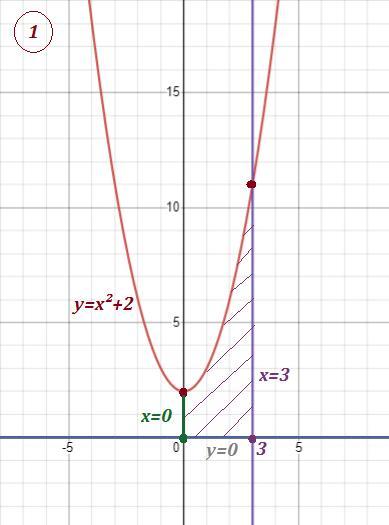
1. Найдите площадь криволинейной трапеции, ограниченной линиями:
y=x²+2, y=0, x=0, x=3
А) 8⅓
Б) 11
В) 3
Г) 15
2. Найти общий вид первообразных для функции f(x)=-5 на промежутке (–∞; +∞)
А) F(x)=5x+C
Б) F(x)=-5x+C
В) F(x)=C
Г) F(x)=-x+C
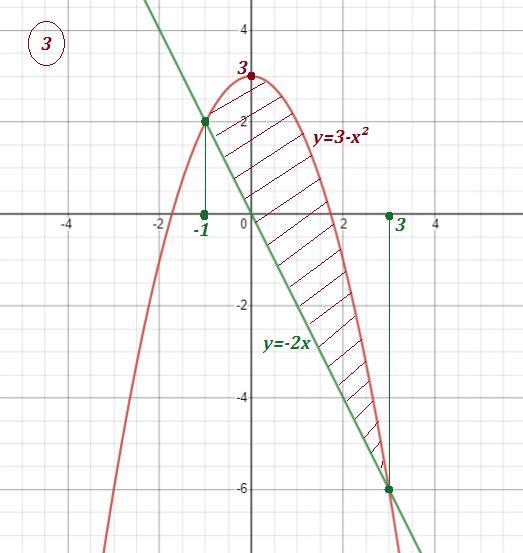
3. Вычислите площадь фигуры, ограниченной линиями:
y=3-x² и y=-2x
А) 15⅓
Б) 1⅔
В) 2⅔
Г) 20⅔

Answer 1

Формула интегрирования степенной функции:

$\int x^ndx=\dfrac{x^{n+1}}{n+1}+C,\ n\neq -1$

1. Для определения площади криволинейной трапеции нужно вычислить определенный интеграл:

$\int_0^3(x^2+2)dx=\left.\left(\dfrac{x^3}{3}+2x\right)\right|_0^3=\left(\dfrac{3^3}{3}+2\cdot3\right)-\left(\dfrac{0^3}{3}+2\cdot0\right)=9+16=15$

2. По формуле интегрирования получим:

$f(x)=-5$

$F(x)=-5x+C$

3. Найдем точки пересечения графиков функций. Для этого решаем уравнение:

$3-x^2=-2x$

$x^2-2x-3=0$

Так как сумма старшего коэффициента и свободного члена равна второму коэффициенту, то:

$x_1=-1;\ x_2=3$

Тогда, необходимо вычислить следующий определенный интеграл:

$\int\limits_{-1}^3(3-x^2-(-2x))dx=\int\limits_{-1}^3(3-x^2+2x)dx=\left.\left(3x-\dfrac{x^3}{3} +\dfrac{2x^2}{2} \right)\right|_{-1}^3=$

$=\left.\left(3x-\dfrac{x^3}{3} +x^2\right)\right|_{-1}^3=\left(3\cdot3-\dfrac{3^3}{3} +3^2\right)-\left(3\cdot(-1)-\dfrac{(-1)^3}{3} +(-1)^2\right)=$

$=\left(9-9+9\right)-\left(-3+\dfrac{1}{3} +1\right)=9+3-\dfrac{1}{3}-1=10\dfrac{2}{3}$

Answer 2

Ответ:

$1)\ \ y=x^2+2\ ,\ \ y=0\ ,\ \ x=0\ ,\ \ x=3\\\\\displaystyle S=\int\limits_0^3\, (x^2+2)\, dx=\Big(\frac{x^3}{3}+2x\Big)\Big|_0^3=\frac{3^3}{3}+2\cdot 3=9+6=15$

Ответ: Г) .

2)  F(x) - первообразная для  y=f(x)  ,  если  $F'(x)=f(x)$  .

$f(x)=-5\\\\F(x)=-5x+C\ ,\ tak\ kak\ \ F'(x)=(-5x+C)'=-5\cdot 1+0=-5=f(x)$

Ответ:  Б) .

$3)\ \ y=3-x^2\ ,\ y=-2x\\\\3-x^2=-2x\ \ \to \ \ \ x^2-2x-3=0\ \ ,\ \ x_1=-1\ ,\ x_2=3\ \ (teorema\ Vieta)\\\\\displaystyle S=\int\limits^3_{-1}\, (3-x^2-(-2x))\, dx=\int\limits^3_{-1}\, (3-x^2+2x)\, dx=\Big(3x-\frac{x^3}{3}+x^2\Big)\Big|_{-1}^3=\\\\\\=(9-9+9)-(-3+\frac{1}{3}+1)=9+2-\frac{1}{3}=11-\frac{1}{3}=10\frac{2}{3}$