Предмет: Геометрия,
автор: eva200713
❗75 баллов❗
Из точки до прямой проведено две наклоны. Одна из них длиной 24√2 см образует прямой угол 45 градусов. Найдите длину второй наклонной, если ее проекция на прямую равна 18 см.
Приложения:
Ответы
Автор ответа:
3
Ответ:
АС=30см
Объяснение:
ДАНО:
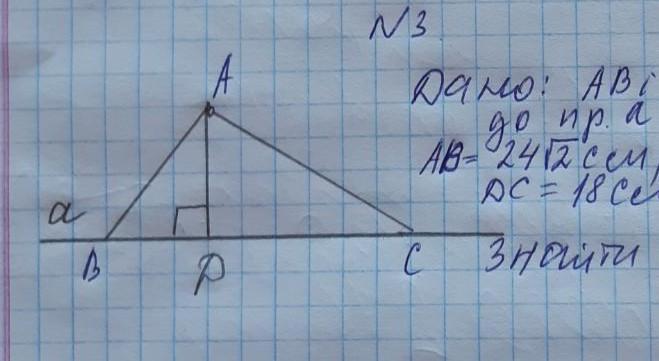
АВ, АС – наклонные, АВ=24√2 см, ∠АВД=45°; ДС=18см
НАЙТИ: АС
РЕШЕНИЕ:
Рассмотрим ∆ВАД, он прямоугольный, где ВД и АД – катеты, а АВ – гипотенуза. Сумма острых углов прямоугольного треугольника равна 90°, поэтому если ∠В=45°, то ∠ВАД=90–∠А=90–45=45°.
∆ВАД – равнобедренный, поэтому ВД=АД.
В равнобедренном прямоугольном треугольнике катет всегда меньше гипотенузы в √2 раз, тогда ВД=АД=24√2÷√2=24см.
В ∆АСД: по теореме Пифагора:
АС²=ДС²+АД²=18²+24²=324+576=900
АС=√900=30см
eva200713:
Спасибо :)
Рада что помогла)
Похожие вопросы
Предмет: Английский язык,
автор: yanochka13kol
Предмет: Другие предметы,
автор: валера885
Предмет: Русский язык,
автор: vizulnastena
Предмет: Литература,
автор: evdok28052910
Предмет: Математика,
автор: SofiaUridia