Решите подробно ! Правильный ответ 544

Ответы
Ответ:
Площадь параллелограмма ABCD равна 544 см².
Объяснение:
Требуется найти площадь параллелограмма.
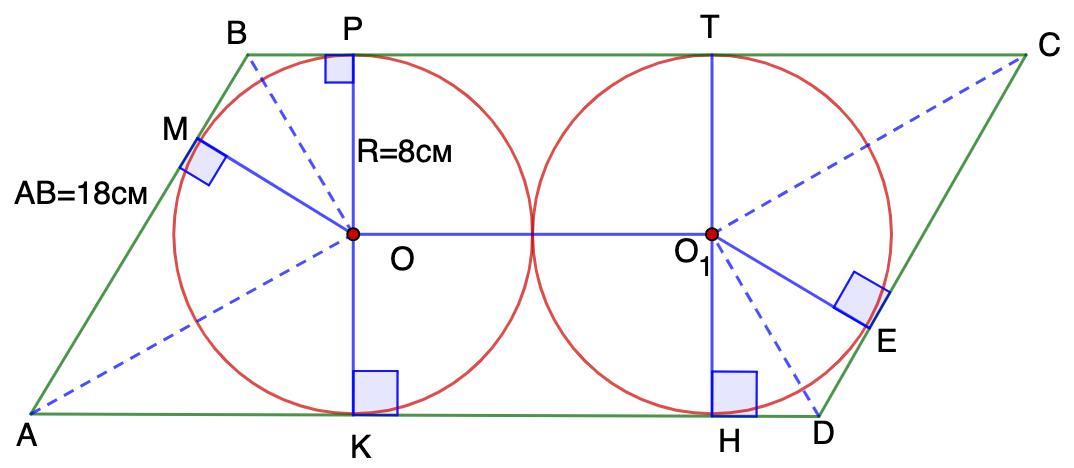
Дано: Окр.О,R; Окр.О₁,R;
ABCD - параллелограмм;
М, Р, Т, Е, Н, К - точки касания.
АВ = 18 см; R = 8 cм.
Найти: S (ABCD)
Решение:
- Площадь параллелограмма равна произведению основания на высоту.
1.
- Отрезки касательных к окружности, проведенные из одной точки, равны.
⇒ МВ = ВР; МА = АК; ТС = ТЕ; ED = DH. (1)
- Противоположные стороны параллелограмма равны.
⇒ АВ = CD = 18см.
или
ВМ + МА = СЕ + ЕD = 18 см
Из равенств (1) ⇒
ВР + АК = ТС + НD = 18 см (2)
2. Рассмотрим ΔАОК и ΔО₁ТС.
- Радиус, проведенный в точку касания, перпендикулярен касательной.
⇒ ΔАОК и ΔО₁ТС - прямоугольные.
- Противоположные углы параллелограмма равны.
⇒ ∠А = ∠С.
- Центр вписанной окружности лежит на биссектрисе угла.
⇒ ∠ОАК = ∠ТСО₁
ОК = ОТ = R
⇒ ΔАОК и ΔО₁ТС (по катету и острому углу)
⇒ АК = ТС (как соответственные элементы).
3. Рассмотрим ΔОВР и ΔHOD.
Аналогично п.2 получим, что ΔОВР = ΔHOD.
⇒ ВР = НD.
4. Перепишем равенство (2)
ВР + АК = ТС + НD = 18 см
или, учитывая п.2 и п.3.:
HD + АК = ВР + ТС = 18 см
5. Рассмотрим КОО₁Н.
ОК = О₁Т = R
- Если две прямые перпендикулярны третьей, то они параллельны между собой.
⇒ ОК || О₁Т
- Если две противоположные стороны четырехугольника равны и параллельны, то этот четырехугольник - параллелограмм.
⇒ КОО₁Н - параллелограмм.
ОО₁ = КН = 2R = 16 см.
6. Найдем высоту и основание параллелограмма.
КР = 2R = 16 см - высота.
AD = AK + HD + KH = 18 + 16 = 34 (см) - основание.
7. Найдем площадь:
S (ABCD) = AD · KP = 34 · 16 = 544 (см²)
Площадь параллелограмма ABCD равна 544 см².
Дальше разбиваем фигуру на три части:
1) квадрат РТНК со стороной 16 см. и площадью 256 см^2;
2 и 3) две одинаковые трапеции АВРК и ТСНД. Расчитаем их площадь на примере трапеции АВРК. Высота трапеции 16 см., и сумма оснований ВР + АК = 18 см. Средняя линия равна полусумме оснований, то есть 9 см. Площадь трапеции 9 × 16 = 144 см^2.
Площадь параллелограмма АВСД равна:
144 + 256 + 144 = 544 см^2.