Предмет: Алгебра,
автор: MythRoid
4.Найдите целые корни многочлена f(x) = x^4-x^3-2x^2-4x-24
5.Решите уравнение методом разложения на множители
Приложения:
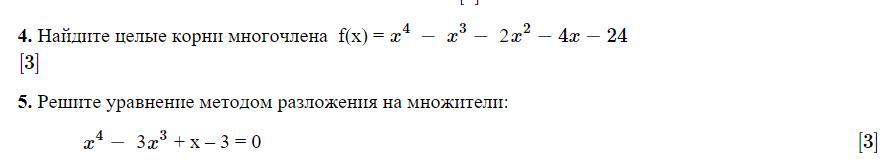
Ответы
Автор ответа:
1
Ответ:
Объяснение:
дискриминант <0, действительных корней нет
Ответ: -1; 3
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: solfkakkamb7
Предмет: Русский язык,
автор: Аноним
Предмет: Алгебра,
автор: kakyla09