дам 50 баллов, 7-ой класс алгебра.
4 уравнения.
не знаю название способа, но вот примерно так:
х²+6х-4=0
(х+3)²-13=0
(х+3)²=13
х+3=√13
х±√13-3
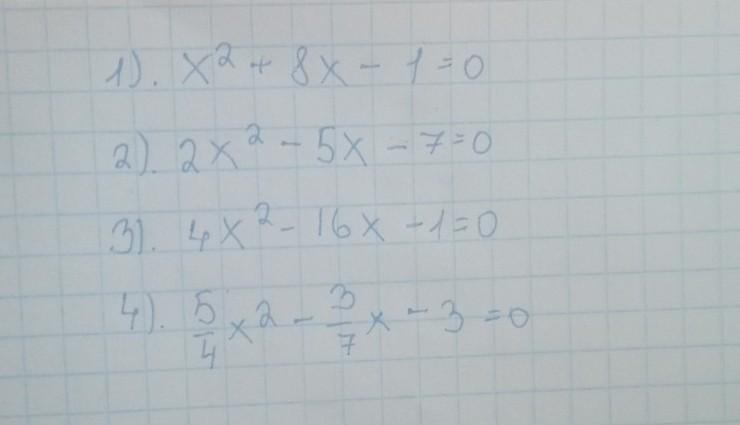
Ответы
Ответ:
В решении.
Объяснение:
Способ называется "выделение полного квадрата).
1) х² + 8х - 1 = 0
х² + 8х + 4² - 4² - 1 = 0
(х + 4)² - 17 = 0
(х + 4)² = 17
х + 4 = ±√17
х = ±√17 - 4;
2) 2х² - 5х - 7 = 0/2
↓
х² - 2,5х - 3,5 = 0
х² - 2,5х + 1,25² - 1,25² - 3,5 = 0
(х - 1,25)² - 5,0625 = 0
(х - 1,25)² = 5,0625
х - 1,25 = ±√5,0625
х - 1,25 = ±2,25
х = -2,25 + 1,25
х₁ = -1;
х = 2,25 + 1,25
х₂ = 3,5;
3) 4х² - 16х - 1 = 0/4
↓
х² - 4х - 0,25 = 0
х² - 4х + 2² - 2² - 0,25 = 0
(х - 2)² - 4,25 = 0
(х - 2)² = 4,25
х - 2 = ±√4,25
х - 2 = ±√(0,25*17)
х - 2 = ±0,5√17
х = ±0,5√17 + 2;
4) 5х²/4 - 3х/7 - 3 = 0/5/4
х² - 12х/35 + (6/35)² - (6/35)² - 2,4 = 0
(х - 6/35)² - 2904/1225 = 0
(х - 6/35)² = 2904/1225
х - 6/35 = ±√(2904/1225)
х - 6/35 = ±√((16*186)/1225)
х - 6/35 = (±4√186)/35
х = (±4√186)/35 + 6/35.
Проверка путём подстановки вычисленных значений х в уравнения показала, что данные решения удовлетворяют данным уравнениям.
1.
2.
3.
4.