Предмет: Алгебра,
автор: adammickevic99
Розв'яжіть систему рівнянь :
Приложения:
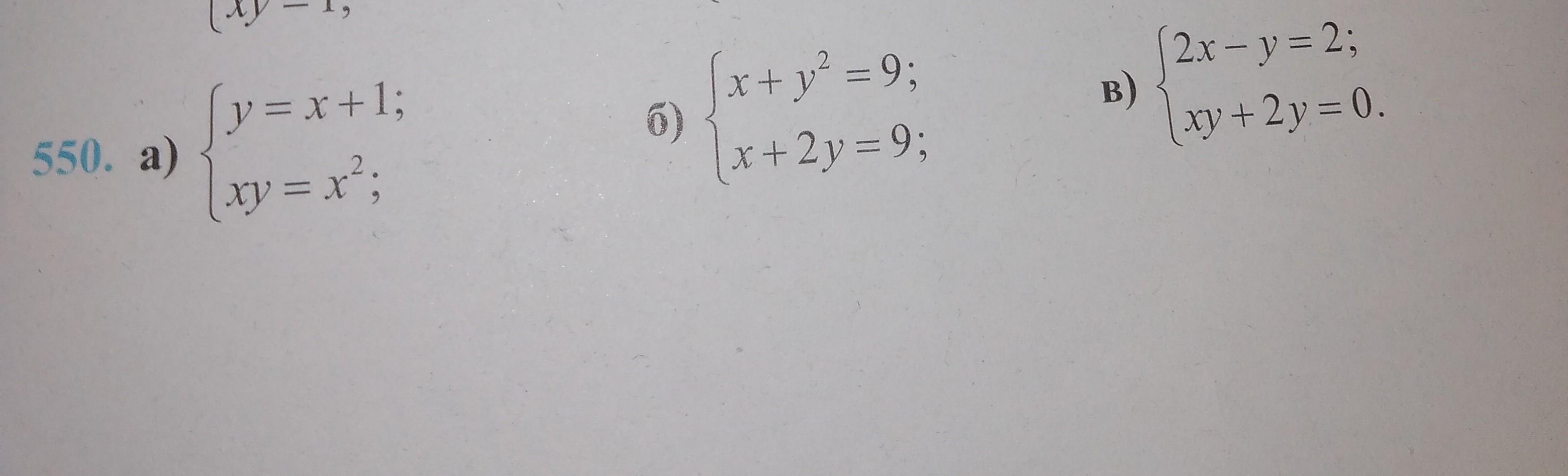
Ответы
Автор ответа:
1
Объяснение:
550.
Ответ: (0;1).
Ответ: (9;0), (5;2).
Ответ: (1;0), (-2;-6).
Похожие вопросы
Предмет: Английский язык,
автор: никмта1д
Предмет: Қазақ тiлi,
автор: EllaRai
Предмет: Английский язык,
автор: Tatiana13000
Предмет: Литература,
автор: bardenik
Предмет: Математика,
автор: zakharsolntzev