Question

биссектриса одного угла треугольника равна биссектрисе его внешнего угла при той же вершине найдите. Найдите разность двух других углов треугольника

Answer 1

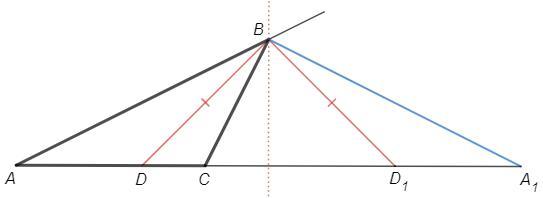
BD, BD1 - биссектрисы

△DBD1 - равнобедренный, серединный перпендикуляр к основанию проходит через вершину B.

Отметим точку A1, симметричную точке A относительно серединного перпендикуляра к DD1.

∠A=∠A1, ∠ABD=∠A1BD1 (симметрия) =∠DBC

Биссектрисы смежных углов перпендикулярны, ∠DBD1=90°

∠A1BC =∠A1BD1+∠CBD1 =∠DBC+∠CBD1 =90°

∠BCA =∠A1BC+∠A1 (внешний угол △A1BC) => ∠BCA-∠A =∠A1BC =90°