Предмет: Алгебра,
автор: akkaowoerjrj
ПОЖАЛУЙСТА УМОЛЯЮ ПОМОГИТЕ ООЧЕНЬ НАДОООООО!!! 37.6 (1;2;3)
Приложения:
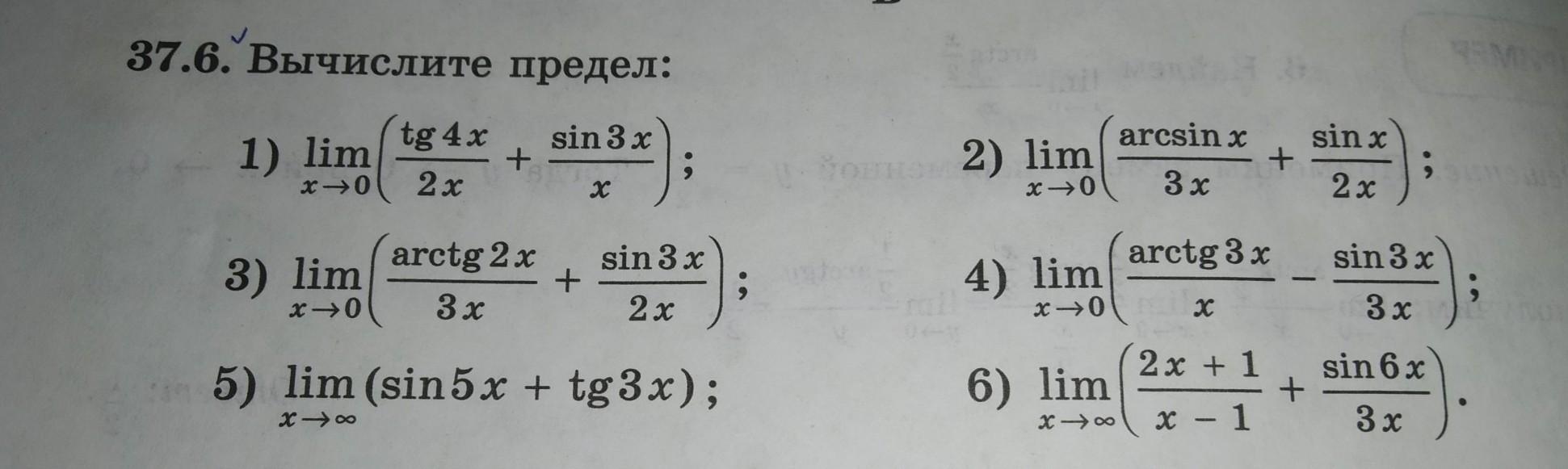
Ответы
Автор ответа:
1
Ответ.
Правило: предел суммы равен сумме пределов. И пользуемся способом замены бесконечно малых величин эквивалентными им .
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Другие предметы,
автор: Аноним
Предмет: Другие предметы,
автор: rina7d69
Предмет: Геометрия,
автор: aly0472