Question

ПОМОГИТЕ ПОЖАЛУЙСТА!!!!!!!!!!!!!!
ПРОШУ ПОМОГИТЕ !!!!!!!!



решение уже есть но нужно записать свойства
во втором файле есть пример свойства

Answer 1

Ответ:

В решении.

Объяснение:

Дана функция у = 3х(2 + х);

                                    ↓

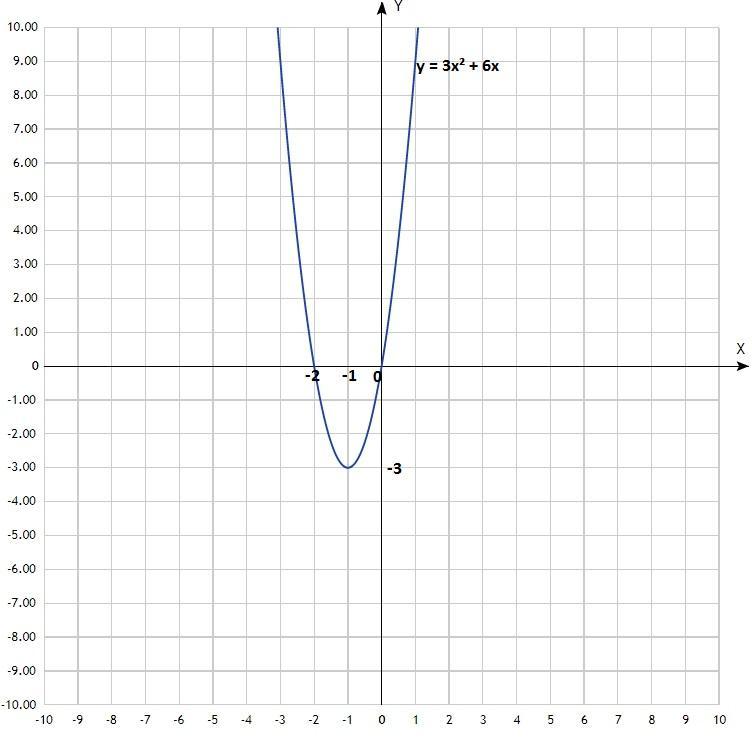
                          у = 3х² + 6х;

Уравнение квадратичной функции, график - парабола со смещённым центром, ветви направлены вверх (коэффициент при х² > 0).

1) Найти координаты вершины параболы:

х₀ = -b/2a;

х₀ = -6/6

х₀ = -1;

Найти у₀:

у = 3х² + 6х;

у₀ = 3 * (-1)² + 6 * (-1) = 3 - 6 = -3

у₀ = -3;

Координаты вершины параболы: (-1; -3).

Ось симметрии = х₀;

Х = -1;

2) Построить график функции. Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.

           у = 3х² + 6х;

           Таблица:

х  -3     -2     -1     0     1

у   9      0     -3     0     9

По вычисленным точкам и координатам вершины построить параболу.

Свойства данной функции:

1) Область определения параболы - множество всех действительных чисел, потому что она проецируется на любую точку оси Ох.

Обычно запись: D(у) = R, или D(у) = х∈(-∞; +∞);

2) Область значений - это проекция графика на ось Оу.

Обозначается как Е(f) или Е(y).

Область значений параболы определяется координатами вершины параболы, конкретно у₀.

у₀ = -3;

Е(у) = у∈[-3; +∞);

3) у = 0 при х = -2;  х = 0, точки пересечения графиком оси Ох, нули функции;

4) у > 0 (график выше оси Ох) при х от -∞ до х= -2 и от х=0 до +∞.

Запись: у > 0 при х∈(-∞; -2)∪(0; +∞);

5) у < 0 (график ниже оси Ох) при х от х= -2 до х= 0;

Запись: у < 0 при х∈(-2; 0);

6) Функция возрастает при х∈(-1; +∞);

7) Функция убывает при х∈(-∞; -1);

8) Функция ограничена снизу ординатой у = -3;

9) у наим. = -3;

10) у наиб. не существует.