розв'язати нерівність даю 90 балів.
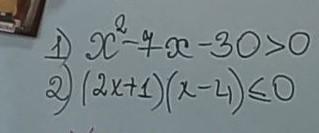
Ответы
Ответ:
В решении.
Объяснение:
Решить неравенство:
1) х² - 7х - 30 > 0;
Приравнять к нулю и решить квадратное уравнение:
х² - 7х - 30 = 0
D=b²-4ac = 49 + 120 = 169 √D=13
х₁=(-b-√D)/2a
х₁=(7-13)/2
х₁= -6/2
х₁= -3;
х₂=(-b+√D)/2a
х₂=(7+13)/2
х₂=20/2
х₂= 10;
Уравнение квадратичной функции, график - парабола, ветви направлены вверх, пересекают ось Ох в точках х= -3 и х=10.
Функция > 0, как в неравенстве, при х от -∞ до х= -3 и от х=10 до +∞ (график выше оси Ох).
Решения неравенства: х∈(-∞; -3)∪(10; +∞).
Неравенство строгое, скобки круглые.
2) (2х + 1)(х - 4) <= 0
2х² - 8х + х - 4 <= 0
2х² - 7х - 4 <= 0
Приравнять к нулю и решить квадратное уравнение:
2х² - 7х - 4 = 0
D=b²-4ac = 49 + 32 = 81 √D=9
х₁=(-b-√D)/2a
х₁=(7-9)/4
х₁= -2/4
х₁= -0,5;
х₂=(-b+√D)/2a
х₂=(7+9)/4
х₂=16/4
х₂=4;
Уравнение квадратичной функции, график - парабола, ветви направлены вверх, пересекают ось Ох в точках х= -0,5 и х=4.
Функция <= 0, как в неравенстве, при х от х = -0,5 до х= 4 (график ниже оси Ох).
Решения неравенства: х∈[-0,5; 4].
Неравенство нестрогое, скобки квадратные.