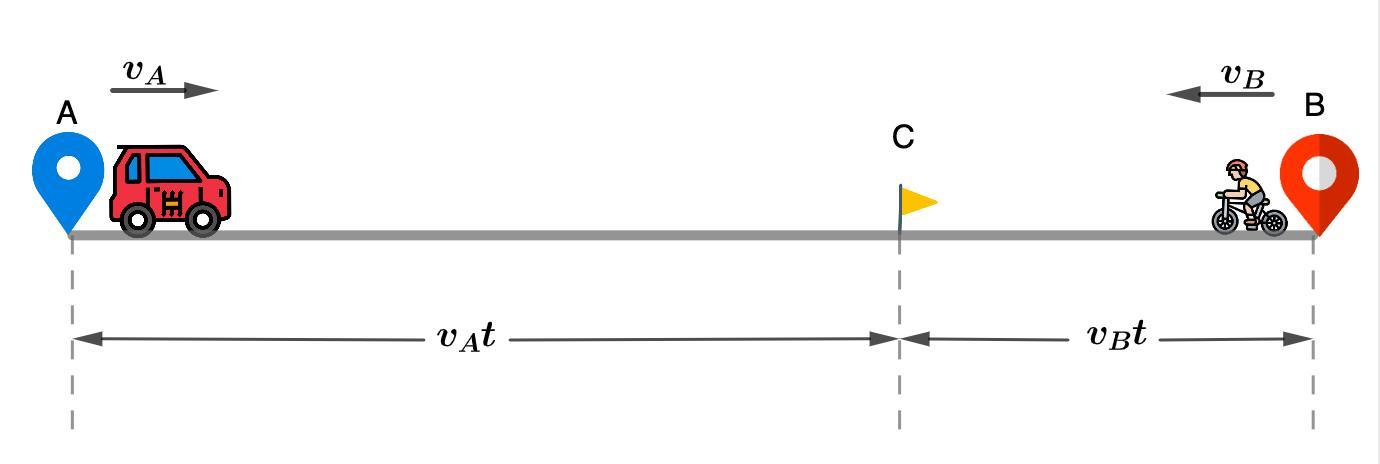
Из пунктов А и B одновременно навстречу друг другу выехали автомобиль (из пункта А) и велосипедист (из пункта В). Во сколько раз скорость автомобиля больше скорости велосипедиста, если после встречи автомобиль ехал еще 1 час до пункта В, а велосипедист ехал еще 9 часов до пункта А?
Ответы
Ответ:
Скорость автомобиля больше скорости велосипедиста в 3 раза.
Пошаговое объяснение:
Требуется найти, во сколько раз скорость автомобиля больше скорости велосипедиста.
По условию:
Из пунктов А и B одновременно навстречу друг другу выехали автомобиль (из пункта А) и велосипедист (из пункта В).
Если автомобиль и велосипедист выехали одновременно, то время до встречи у них будет одинаковое.
Пусть скорость автомобиля - км/ч;
скорость велосипедиста - км/ч.
Время до встречи - ч.
С - место встречи.
Формулы расстояния и скорости:
Тогда расстояния:
км
км
После встречи расстояние ВС автомобиль проедет за 1 час.
Следовательно, его скорость будет равна
(км/ч)
Велосипедист после встречи проехал расстояние АС за 9 часов.
Значит, его скорость равна
(км/ч)
Найдем отношение скоростей автомобиля и велосипедиста:
По свойству пропорции:
Получили, что скорость автомобиля больше скорости велосипедиста в 3 раза.