Предмет: Алгебра,
автор: gagagagogogo69
упростите выражение
Приложения:
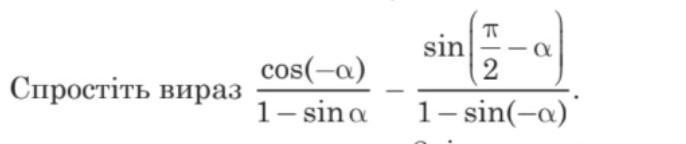
Ответы
Автор ответа:
1
Мы воспользовались формулами
(четность косинуса);
(нечетность синуса);
(формула приведения);
(формула сокращенного умножения);
(определение тангенса).
Похожие вопросы
Предмет: Английский язык,
автор: диля143
Предмет: Українська мова,
автор: стас2404
Предмет: Русский язык,
автор: vladikdroid
Предмет: Қазақ тiлi,
автор: balakarev06
Предмет: Алгебра,
автор: Гуля551