помогите решить пожалуста
Ответы
Ответ:
350
Пошаговое объяснение:
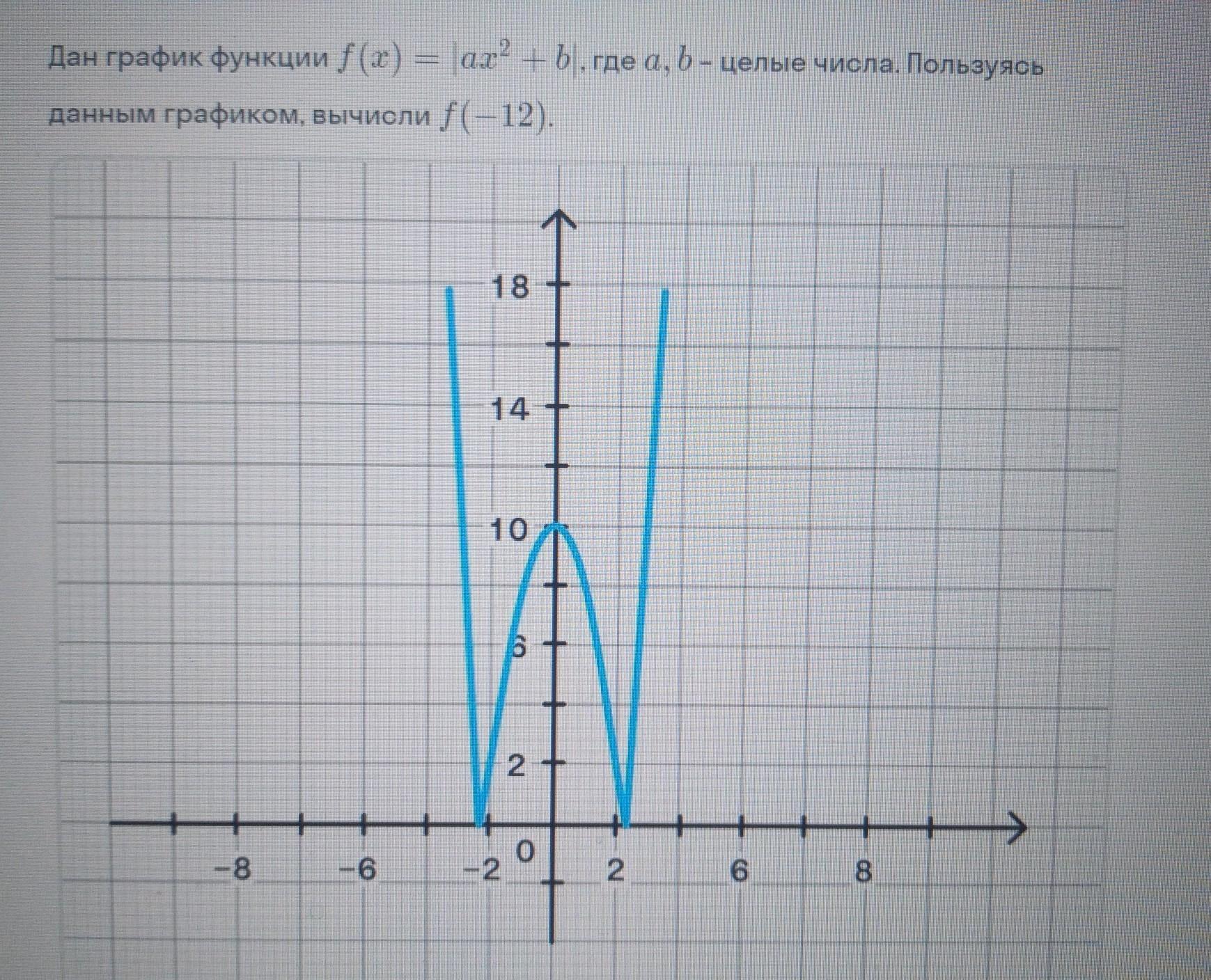
1) Находим координаты точек, через которые проходит парабола, согласно уравнению под знаком модуля.
Первые две точки:
(-2; 0) и (2; 0).
Третья точка (0; 10) является зеркальным отражением точки (0;-10), так уравнение под знаком модуля.
2) Значит, можно указать координаты 3-х точек, через которые проходит парабола, стоящая под заком модуля:
А (-2; 0)
В (0; -10)
С (2; 0).
3) Для каждой из этих точек, пользуясь заданных уравнением у = аx² + b, можно соответственно составить следующие верные равенства:
0 = аx² + b = а (-2)² + b (1)
-10 = аx² + b = а (0)² + b (2)
0 = аx² + b = а (2)² + b (3)
4) Из уравнения (2) следует, что b = -10, значит, подставив в уравнение (1) или (2) вместо b его значение (-10), найдём, чему равно а:
0 = а (-2)² - 10 = а · 4 - 10
4а = 10
а = 2,5
5) Зная а и b, составляем уравнение параболы под знаком модуля (пока не обращая внимания на знак модуля):
у = 2,5х² - 10
6) Находим, чему равен у, когда х = -12:
у = 2,5 · (-12)² - 10 = 2,5 · 144 - 10 = 360 - 10 = 350
Теперь берём модуль:
|350| = 350
Ответ: 350
ПРИМЕЧАНИЕ: рисунок в задании дан не в масштабе. На нём правильные только те 3 точки, которые я привёл в решении. На остальные ориентироваться нельзя, так как на самом деле ветви идут намного ближе к оси х.
Ответ: f(-12) =278
Пошаговое объяснение: y=|ax²+b|, причём a, b∈Z
1)Для построения графика функции y=|ax²+b| сначала был построен график функции у=ax²+b, а затем часть параболы, расположенную в нижней полуплоскости, отобразили симметрично относительно оси ОХ
2) Следовательно вершина параболы у=ax²+b находится в точке (0;-10), т.е. b=-10;
3) абсциссы точек пересечения с осью абсцисс на графике удовлетворяет условию: 2<|x|<3
4) Найдём точки пересечения параболы у= ах²-10 с осью абсцисс:
ах²-10=0
ах²=10
х²=10/а
Но по условию а∈Z, х²≥0; значит возможно ,
что а=10; 9; 8; 7; 6; 5; 4; 3; 2;1.
Если а=10, то х²=10/10 = 1, ⇒х=±1 (что не соответствует графику на рисунке)
Если а=10, то х²=10/10 = 1, ⇒х=±1 (что не соответствует графику на рисунке)
Если а=9, то х²=10/9 = 2, ⇒х=±√10/3 (что не соответствует графику на рисунке; абсциссы точек пересечения на рисунке по модулю больше 2, но меньше 3)
Если а=8, то х²=10/8=5/4 = 1, ⇒х=±√5/2 (что не соответствует графику на рисунке, √5/2≈1,1)
Если а=5, то х²=10/5=2, ⇒х=±√2 (что не соответствует графику на рисунке, √2≈1,4)
Если а=2, то х²=10/2 = 5, ⇒х=±√5, причём 2< |±√5 |<3
Это значит, что а=2, b= -10
5) Функция задана формулой f(x)=|2x² - 10|
6) Тогда f(-12)= | 2·(-12)²-10|= | 2·144-10|=278