Question

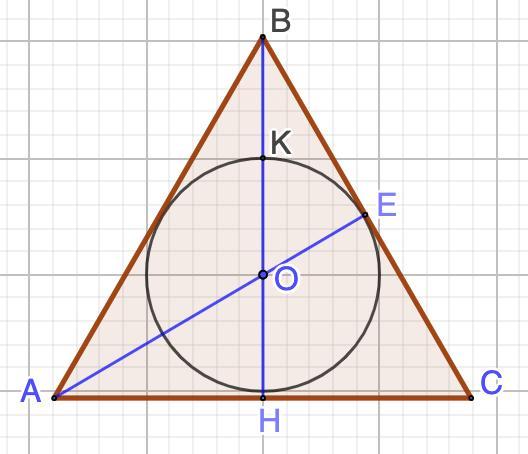
Окружность с центром в точке O вписана в правильный треугольник ABC . Найди диаметр вписанной окружности, если BO=13 .

Answer 1

Ответ:

Диаметр вписанной окружности равен 13 (ед.)

Объяснение:

Требуется найти диаметр вписанной окружности в правильный треугольник.

Дано: ΔАВС - правильный;

Окр.О - вписанная в ΔАВС;

ВО = 13.

Найти: Диаметр вписанной окружности.

Решение:

• Центр вписанной окружности лежит на биссектрисе угла.

⇒ ВН - биссектриса.

• В правильном треугольнике биссектриса, проведенная к любой стороне, является его медианой, высотой.

⇒ ВН - медиана, высота.

• Радиус, проведенный в точку касания, перпендикулярен касательной.

⇒ ОН - радиус.

• Медианы точкой пересечения делятся в отношении 2 : 1, считая от вершины.

⇒ ВО : ОН = 2 : 1

То есть ВО в два раза больше ОН.

ВО = 13 ед.;

⇒ ОН = ВО : 2 = 13 : 2 = 6,5 (ед.)

• Длина диаметра равна длине двух радиусов.

⇒ КН = ОН · 2 = 6,5 · 2 = 13 (ед.)

Диаметр вписанной окружности равен 13 (ед.)