Предмет: Алгебра,
автор: Аноним
Пожалуйста помогите дам 50 баллов
Номер 548 и 549
Приложения:
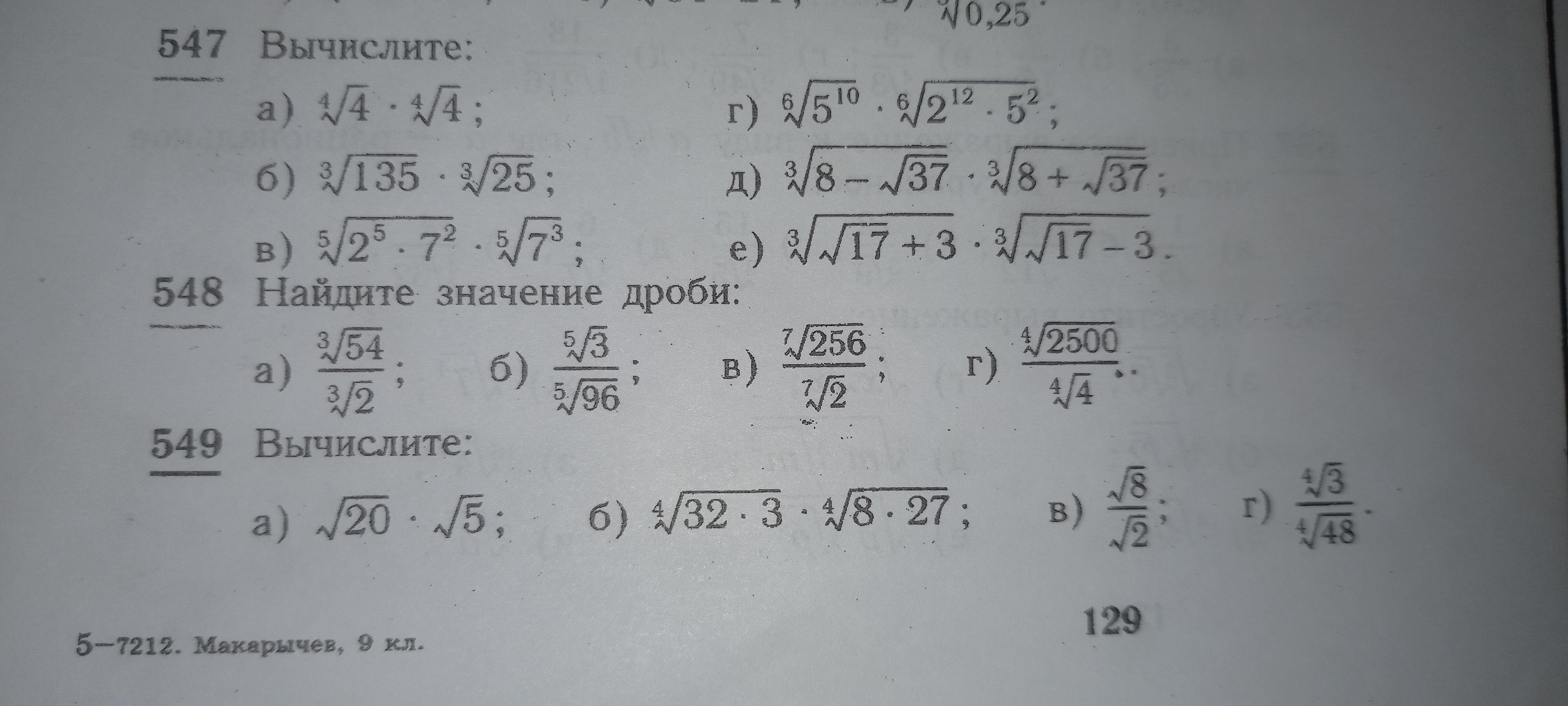
Ответы
Автор ответа:
1
Ответ:
Свойства корней и степеней .
548)
549)
ropenope361:
помогите пожалуйста мне в профиле в вопросах
нужно решить квадратные уравнения
Похожие вопросы
Предмет: Українська мова,
автор: lhasota84
Предмет: Другие предметы,
автор: Аноним
Предмет: Қазақ тiлi,
автор: Ходжаева10
Предмет: Информатика,
автор: romanzubko2007
Предмет: Геометрия,
автор: lampa3123