Предмет: Алгебра,
автор: jakakdnfkdk
Помогите, пожалуйста, с неравенством
Приложения:
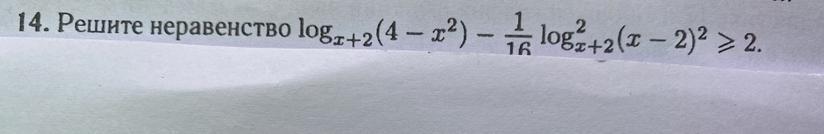
Ответы
Автор ответа:
2
Ответ:
Объяснение:
в условиях одз:
возможно только равенство нулю
Похожие вопросы
Предмет: Английский язык,
автор: neznika2005
Предмет: Другие предметы,
автор: LadLivnerog
Предмет: Английский язык,
автор: Amishkadurdieva
Предмет: Биология,
автор: wertery93
Предмет: Алгебра,
автор: SOVIA111