Предмет: Геометрия,
автор: leilabirzova
Поиск стороны
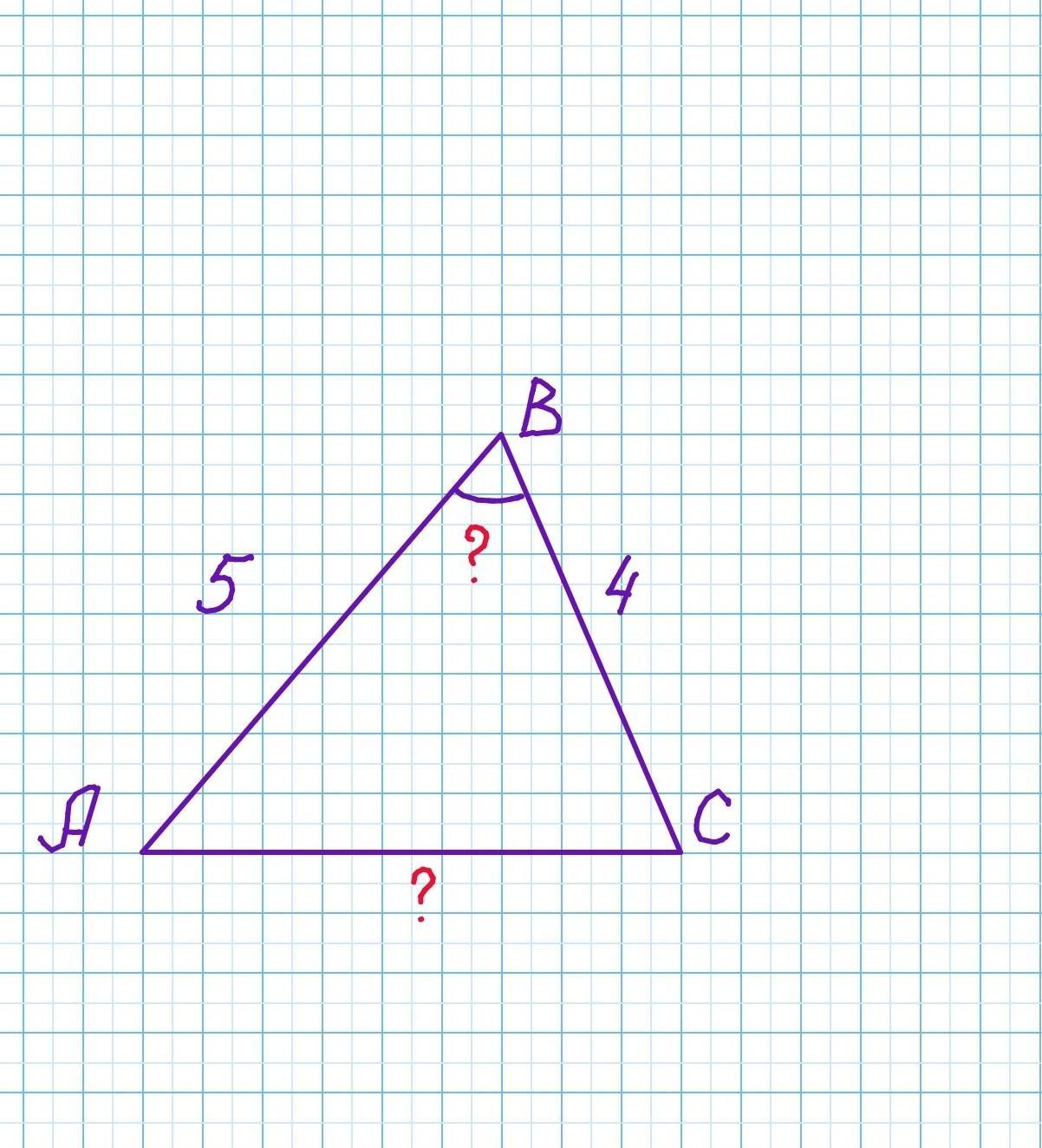
Площадь треугольника ABC равна  , а его стороны AB и BC соответственно равны 5 и 4. Известно, что угол B - острый.
, а его стороны AB и BC соответственно равны 5 и 4. Известно, что угол B - острый.
1) Найдите градусную меру угла В .
2) Найдите AC . Полученный ответ возведите в квадрат.
Ответы
Автор ответа:
0
Ответ:
1)∠В=60°
2)АС²=21
Объяснение:
1) Если известно две стороны треугольника и угол между ними, то площадь данного треугольника вычисляется, как половина произведения этих сторон умноженная на синус угла между ними.
Подставим известные величины в формулу и найдём угол В:
Тогда ∠В=60°.
2)Теорема косинусов: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.
АС²=АВ²+ВС²-2•АВ•ВС•cos60°=5²+4²-2•5•4•½=25+16-20=21
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: тоан7787
Предмет: Русский язык,
автор: koroleva2008
Предмет: Другие предметы,
автор: МарияHAPPY22
Предмет: Математика,
автор: dolorpggg345
Предмет: Литература,
автор: PolinaTyan1