Предмет: Алгебра,
автор: ToTaLoNeT2052
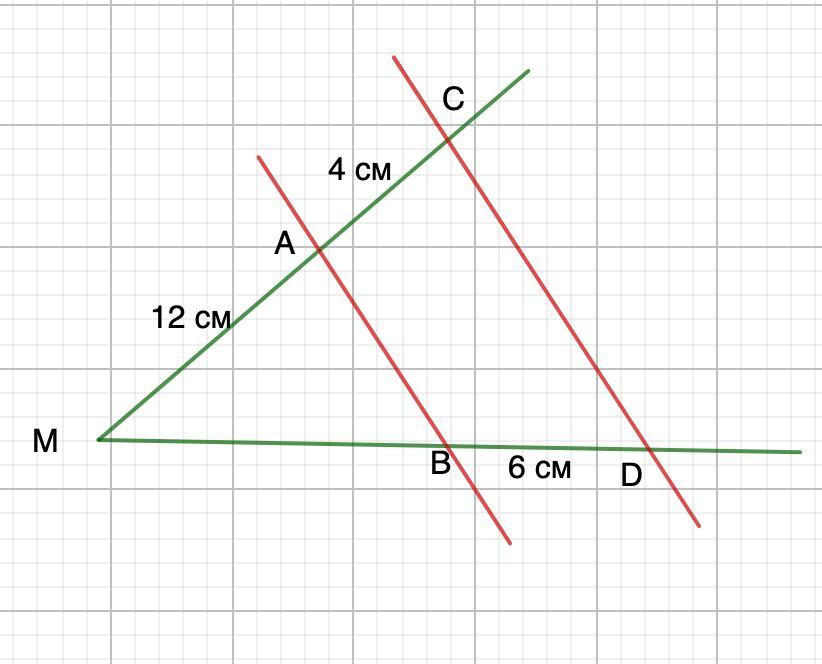
стороны угла М пересекают параллельные прямые AB и CD (точка А между М и С) МА=12см, АС=4см, ВD=6см. Найдите отрезок MB.
Ответы
Автор ответа:
1
Ответ:
Отрезок MB равен 18 см.
Объяснение:
Требуется найти отрезок МВ.
Дано: ∠М;
AB || CD;
МА=12см, АС=4см; ВD=6см.
Найти: МВ.
Решение:
- Теорема о пропорциональных отрезках:
- Если параллельные прямые пересекают стороны угла, то отрезки, образовавшиеся на одной стороне угла, пропорциональны соответствующим отрезкам, образовавшиеся на другой стороне угла.
По условию имеем ∠М и AB || CD
Запишем пропорцию:
Подставим данные значения отрезков МА=12 см, АС=4 см; ВD=6 см в пропорцию:
- Основное свойство пропорции: произведение крайних членов равно произведению средних.
Отрезок MB равен 18 см.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: magicwinnie123
Предмет: Другие предметы,
автор: DJSVET
Предмет: Алгебра,
автор: Аноним
Предмет: Информатика,
автор: JokerOP