Question

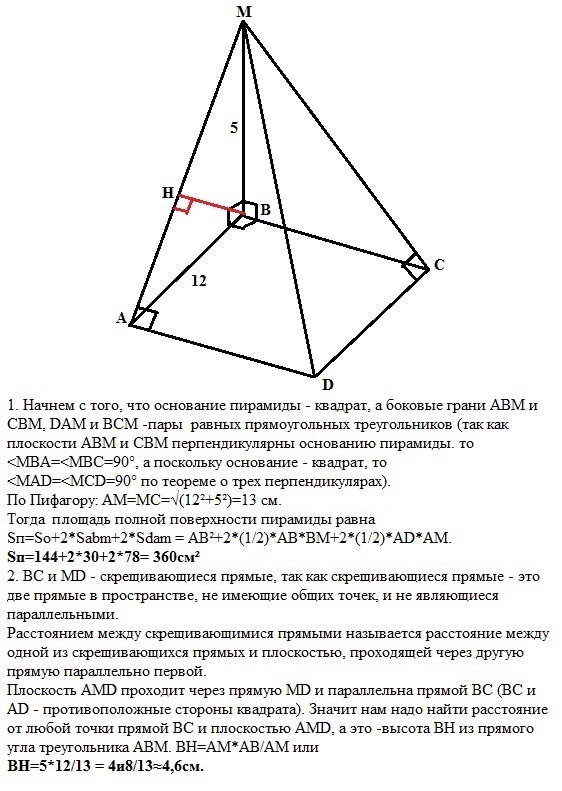
В основании пирамиды MABCD лежит квадрат ABCD со стороной, равной 12. Грани MBA и MBC перпендикулярны к плоскости основания. Высота пирамиды равна 5. Найдите площадь полной поверхности пирамиды. + В указанной выше пирамиде найдите расстояние между прямыми BC и MD.

Answer 1

1. Начнем с того, что основание пирамиды - квадрат, а боковые грани АВМ и СВМ, DAM и ВСМ -пары  равных прямоугольных треугольников (так как плоскости АВМ и СВМ перпендикулярны основанию пирамиды. то  <MBA=<MBC=90°, а поскольку основание - квадрат, то
<MAD=<MCD=90° по теореме о трех перпендикулярах).
По Пифагору: АМ=МС=√(12²+5²)=13 см.
Тогда ллощадь полной поверхности пирамиды равна
Sп=So+2*Sabm+2*Sdam = AB²+2*(1/2)*AB*BM+2*(1/2)*AD*AM.
Sп=144+2*30+2*78= 360cм²
2. ВС и MD - скрещивающиеся прямые, так как скрещивающиеся прямые - это две прямые в пространстве, не имеющие общих точек, и не являющиеся параллельными.
Расстоянием между скрещивающимися прямыми называется расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой.
Плоскость АМD проходит через прямую MD и параллельна прямой ВС (ВС и AD - противоположные стороны квадрата). Значит нам надо найти расстояние от любой точки прямой ВС и плоскостью АМD, а это -высота ВН из прямого угла треугольника АВМ. ВН=АМ*АВ/АМ или
ВН=5*12/13 = 4и8/13≈4,6см.