Предмет: Математика,
автор: milenakarapetyan0507
ДАМ 50 БАЛЛОВ
СРОЧНО
Приложения:
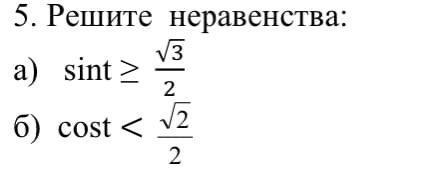
Ответы
Автор ответа:
0
Ответ:
а) π/3 + 2πk ≤ t ≤ 2π/3 + 2πk, k - целое
б) π/4+ 2πk < t < 7π/4 + 2πk, k - целое
Пошаговое объяснение:
а) sin t ≥ √3/2
sin t = √3/2 при t = π/3 и t=2π/3
Значит неравенство sin t ≥ √3/2 выполняется на отрезке [π/3; 2π/3], что эквивалентно двойному неравенству π/3 ≤ t ≤ 2π/3
С учётом периода синуса 2π, записываем ответ
Ответ: π/3 + 2πk ≤ t ≤ 2π/3 + 2πk, k - целое
б) cos t < √2/2
cos t = √2/2 при t = π/4 и t = 7π/4
Значит неравенство cos t < √2/2 выполняется на интервале (π/4; 7π/4), что эквивалентно двойному неравенству π/4 < t < 7π/4
С учётом периода косинуса 2π, записываем ответ
Ответ: π/4+ 2πk < t < 7π/4 + 2πk, k - целое
Похожие вопросы
Предмет: Қазақ тiлi,
автор: МамаМиленыИромы
Предмет: Русский язык,
автор: иванякимов
Предмет: Английский язык,
автор: alenoches
Предмет: Українська мова,
автор: letsrock55
Предмет: Биология,
автор: timur8231