ПОМОГИТЕ СРОЧНО ПОЖАЛУЙСТА
Ответы
Ответ:
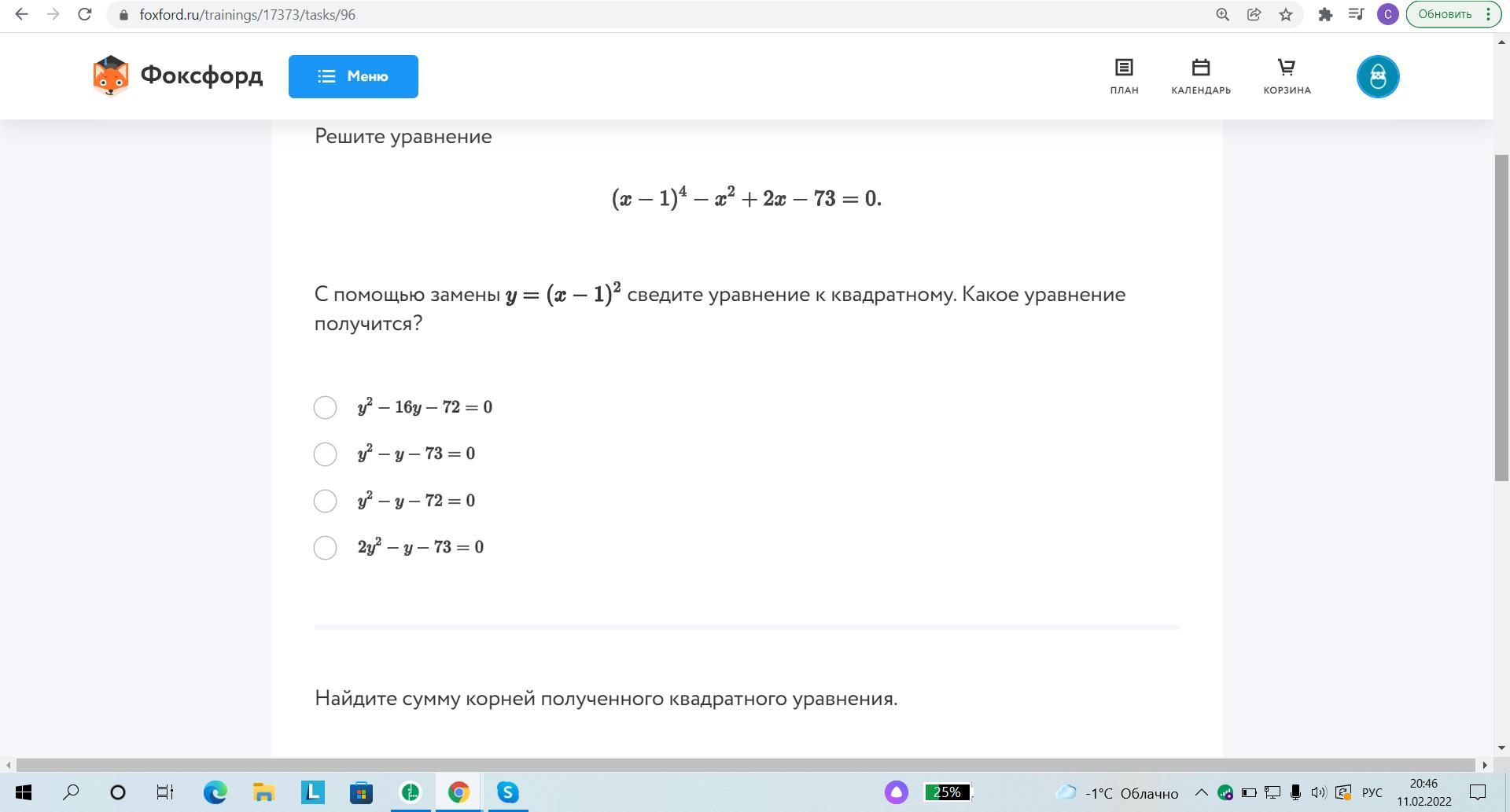
Если применить замену y=(x-1)², то получится квадратное уравнение y²-y-72=0
Сумма корней полученного квадратного уравнения равна 1.
Дополнительно:
(Уравнение четвертой степени имеет корни равные -2 и 4).
Объяснение:
(x-1)⁴-x²+2x-73=0
По условию задачи с помощью замены у=(х-1)² надо привести уравнение к квадратному.
(х-1)²=х²-2х+1
Заметим, что -73 можно представить как -1-72
(x-1)⁴-x²+2x-1-72=0
Теперь, выделим квадрат разности
(x-1)⁴-(x²-2x+1) -72=0
(х-1)⁴-(х-1)²-72=0
Замена: у=(х-1)²
у²-у-72=0
Полученное квадратное уравнение является приведённым, т.к. коэфффициент при у² равен 1, поэтому, по теореме Виета сумма корней уравнения равна второму коэффициенту, взятому с обратным знаком:
у₁+у₂=-(-1)=1
у₁+у₂= 1
Дополнительно:
Произведение корней этого квадратного уравнения равно -72 (по теореме Виета), поэтому, корни уравнения равны -8 и 9.
Обратная замена:
1) (х-1)²=-8
Решений нет, т.к. квадрат числа не может быть отрицательным
2) (х-1)²=9
√(х-1)²=√9
|x-1|=3
х-1=3 и х-1=-3
x₁=4 x₂=-2