Предмет: Алгебра,
автор: viktoriakorepanova32
Необходимо сократить дроби
Приложения:
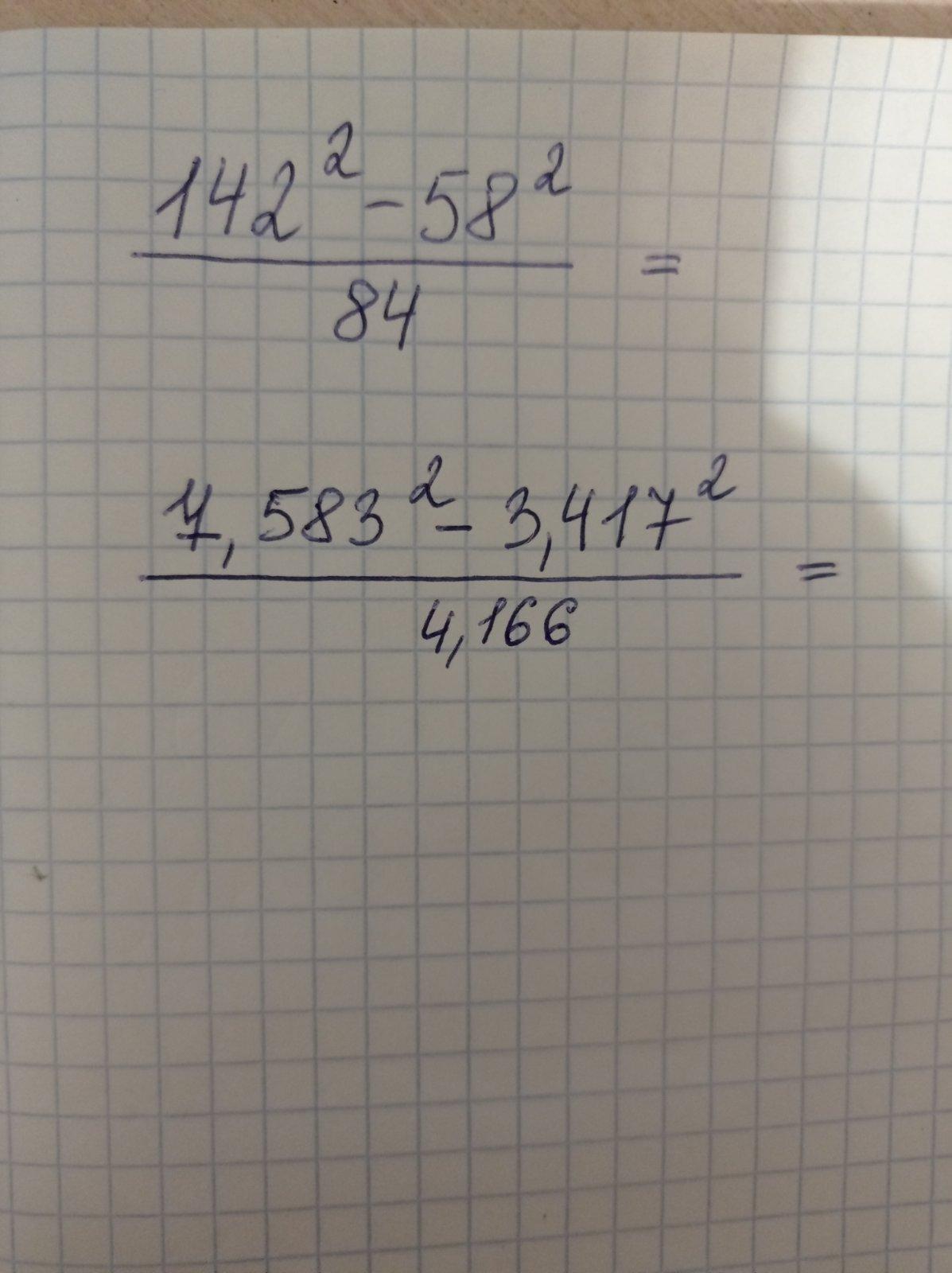
Ответы
Автор ответа:
0
Ответ:
1)200 2)11
Объяснение:
Автор ответа:
1
Ответ:
1) 200
2) 11
Объяснение:
1) у нас есть вот такая дробь
по формуле разложим выражение
получаем дробь
142-58=84
142+58=200
получится дробь , 84 и 84 сокращаются и мы получаем число
.
2) здесь всё посложнее, так как числа не целые.
предлагаю записать эти числа в виде дробей
получим:
теперь нам нужно возвести в степень эти дроби
что бы возвести дробь в степень нужно возвести знаменатель и числитель
путём долгих вычислений мы получим вот такое выражение:
4166*11000 = 45826000
сокращаем 45826000 и 1000 на 1000, получим уже не такое пугающее число
в первой дроби сокращаем на 2, получаем
500 сокращается, получаем
ответом будет число .
dukefissura:
Извиняюсь за довольно запутанное решение во 2 примере.
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: Гомен1029
Предмет: Английский язык,
автор: vikakupina
Предмет: История,
автор: nikita52168
Предмет: Информатика,
автор: suprunenko1