ПОМОГИТЕ ПОЖАЛУЙСТА
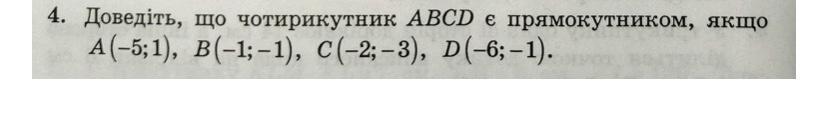
Ответы
Дано:
точки
А(-5; 1) В(-1; -1) С(-2; -3) В(-6; -1)
Доказать, что АВСD - прямоугольник.
------------------------------------------------------------
Доказательство:
Прямоугольник - это параллелограмм, у которого все углы прямые.
Докажем сначала, что АВСD - параллелограмм.
Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны
Уравнение прямой АВ
4(y - 1) = -2(x + 5)
4y + 2x + 6 = 0
или
2у + х + 3 = 0
или
у = -0,5х -1,5.
Угловой коэффициент прямой АВ равен k = - 0.5
Уравнение прямой CD
-4(y + 3) = 2(x + 2)
4y + 2x + 16 = 0
или
2у + х + 8 = 0.
или
у = -0,5х - 4.
Угловой коэффициент прямой CD равен k = - 0.5
Прямые параллельны, если их угловые коэффициенты равны
Следовательно, АВ ║ CD
Уравнение прямой ВС
-(y + 1) = -2(x + 1)
y - 2x - 1 = 0
или
у = 2х + 1.
Угловой коэффициент прямой BC равен k = 2
Уравнение прямой AD
(y + 1) = 2(x + 6)
y - 2x + 11 = 0
или
у = 2х - 11.
Угловой коэффициент прямой AD равен k = 2
Прямые параллельны, если их угловые коэффициенты равны
Следовательно, BC ║ AD
У четырёхугольника ABCD противоположные стороны попарно параллельны: АВ ║ CD и BC ║ AD, следовательно,
АВСD - параллелограмм.
Докажем, что прямые АВ и ВС перпендикулярны.
Две прямые перпендикулярны, если произведение их угловых коэффициентов равно - 1.
Угловой коэффициент прямой АВ равен k₁ = - 0.5
Угловой коэффициент прямой BC равен k₂ = 2
Произведение угловых коэффициентов прямых АВ и ВС
k₁ · k₂ = -0.5 · 2 = -1
Следовательно, АВ ⊥ ВС
Вычисляя произведение угловых коэффициентов прямых ВС и СD , а также прямых CD и AD, получим, что
ВС ⊥ СD и CD ⊥AD
То есть все углы параллелограмма АВСD прямые.
Следовательно, АВСD - прямоугольник