Question

Высота правильной четырехугольной усеченной пирамиды равна 6 см. Объем ее равен 152 см в кубе. Отношения площадей ее оснований 4 на 9 определите площадь боковой поверхности усечённой пирамиды

Answer 1

Высота правильной четырехугольной усеченной пирамиды равна 6 см. Объем ее равен 152 см в кубе. Отношения площадей ее оснований 4 на 9 определите площадь боковой поверхности усечённой пирамиды

Ответ:

Sбок=80√10см²

Пошаговое объяснение:

Площадь нижнего основания обозначим S, a верхнего $S_1$.

Тогда согласно условия:

$\dfrac{S_1}{S} = \dfrac{S(A_1B_1C_1D_1)}{S(ABCD)} = \dfrac{4}{9} \\ \\ \Rightarrow S_1= \frac{4S}{9}$

Объем усеченной пирамиды вычисляется по формуле:

$V= \frac{1}{3} h(S_1 + S + \sqrt{S_1 \times S} )$

V=152 см³, h= 6см.

Подставим в данную формулу известные значения и найдём площадь нижнего основания S:

$\frac{1}{3} \times 6 \times ( \frac{4S}{9} + S + \sqrt{ \frac{4S}{9} \times S } ) = 152 \\ \\ \frac{4S + 9S}{9} + \frac{2S}{3} = 304 \\ \\ \frac{13S + 6S}{9} = 304 \\ \\ 19S = 2736 \\ \\ S = 144$

Площадь нижнего основания равна 144см²

Тогда площадь верхнего основания:

$S_1= \dfrac{4 \times 144}{9} = 64$

Площадь верхнего основания 64 см².

Усечённая пирамида по условию является правильной. Значит в основании лежат правильные четырёхугольники - квадраты.

Площадь квадрата равна: S= a², где а - сторона квадрата.

Тогда длина стороны нижнего основания:

$a = \sqrt{S} = \sqrt{144} = 12$ см

а верхнего:

$a_1 = \sqrt{S_1} = \sqrt{64} = 8$ см

Периметр квадрата находится по формуле: Р=4а.

Периметр нижнего основания:

$P=4a=4 \times 12 = 48$ см

Периметр верхнего основания:

$P_1=4 \times a_1 = 4 \times 8=32$ см

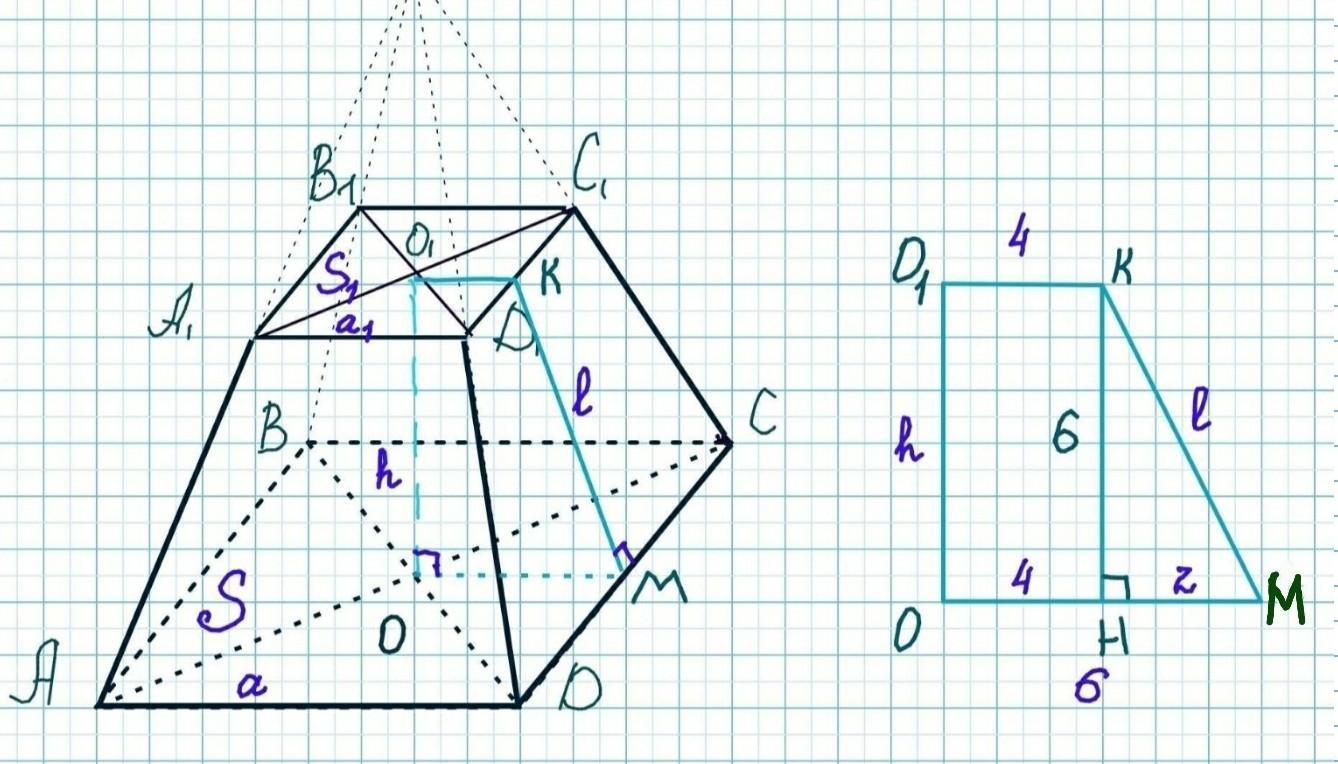
Найдём высоту боковой грани пирамиды - апофему.

Проведём из центров оснований перпендикуляры О1К и ОМ к соответственным сторонам оснований. Это расстояния от центра до боковой стороны.

Для нижнего основания оно равно 6 см (половина стороны основания:

ОМ=½•а=½•12=6 см)

Для верхнего основания: О1К=½•8=4 см

Опустим перпендикуляр КН из точки К на нижнее основание. Получим прямоугольный треугольник КНМ. Катет НМ равен разнице расстояний от центров оснований до боковых сторон: НМ=ОМ-О1К=6-4=2см.

Катет КН= ОО1=h=6см

По теореме Пифагора найдём гипотезу (апофему) КМ:

КМ²=КН²+НМ²=6²+2²=36+4=40

l =КМ=2√10 см

Площадь боковой поверхности усечённой пирамиды находится по формуле:

S= ½•(P1+P)×l = ½ • (32+48) • 2√10 = 80√10 см²

P - периметр нижнего основания,

Р1 - периметр верхнего основания,

l - апофема.

Площадь боковой поверхности усечённой пирамиды равна 80√10 см².