Предмет: Алгебра,
автор: Аноним
Изменится ли значение дроби, если каждое из значений X и Y удвоить:
здесь четыре примера
помогите
Приложения:
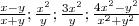
Ответы
Автор ответа:
0
Ответы внизу. Удачи
Приложения:

Автор ответа:
0
Решение:
Удвоим значения х и у
Значение дроби не изменилось
Удвоим значения х и у
Значение дроби увеличилось в 2 раза
Удвоим значения х и у
Значение дроби увеличилось в 2 раза
Удвоим значения х и у
Значение дроби не изменилось
Похожие вопросы
Предмет: Алгебра,
автор: anastasiaivanova5160
Предмет: Қазақ тiлi,
автор: fedotovaannetta
Предмет: Английский язык,
автор: Аноним
Предмет: Геометрия,
автор: 14Анастасия14
Предмет: Информатика,
автор: a1n0n1a8