Question

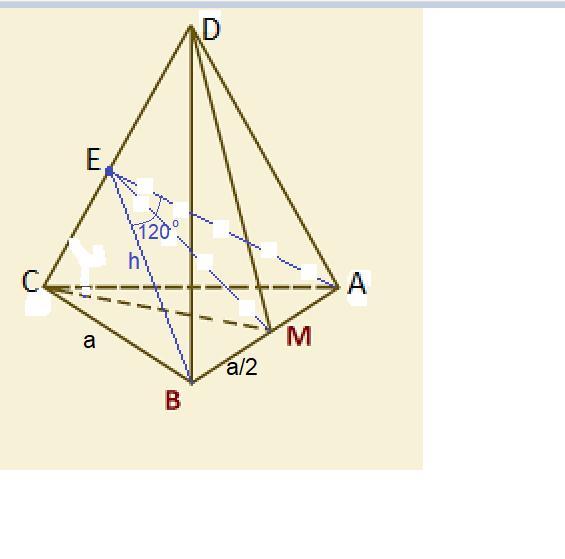
В правильной пирамиде сторона основания равна а, угол между смежными боковыми гранями равен 120 градусов. Определить площадь боковой поверхности пирамиды, если пирамида треугольная.

Answer 1

Начинать надо с заданного угла между боковыми гранями.

Находим высоту h из вершины основания на боковое ребро.

h = (a/2)/sin(120/2) - (a/2)/(√3/2) = a√3/3.

отсюда находим синус угла С при основании боковой грани.

sin C = h/a = (a√3/3)/a = √3/3.

cos C = √(1 - (√3/3)²) = √(1 - (1/3) = √2/√3.

tg C = sin C/cos C = (√3/3)/(√2/√3) = 1/√2 = √2/2.

Теперь можно определить апофему А = DM боковой грани.

A = (a/2)*tgC = (a/2)*(√2/2) = a√2/4.

Площадь боковой поверхности пирамиды находим по формуле:

Sбок = (1/2)РА = (1/2)*(3а)*(a√2/4) = а²*3√2/8.